Calcular Correlações
Se você não apenas deseja interpretar a força da relação, mas também a direção da relação, você pode calcular a correlação.
Neste bloco de aprendizado, dois coeficientes de correlação são apresentados:
r de Pearson
\(\rho\) de Spearman
Para calcular o r de Pearson, as seguintes condições devem ser atendidas:
Variáveis (pseudo-)métricas
Relação linear (monótona)
Igualdade de variância
(Distribuição normal bivariada)
Para calcular o \(\rho\) de Spearman, por outro lado, apenas as seguintes condições precisam ser atendidas:
Variáveis (pelo menos) ordinais
Relação monótona
Relações Lineares e Não Lineares
Na figura, são apresentados quatro exemplos que dariam quase os mesmos valores estatísticos (Quarteto de Anscombe).
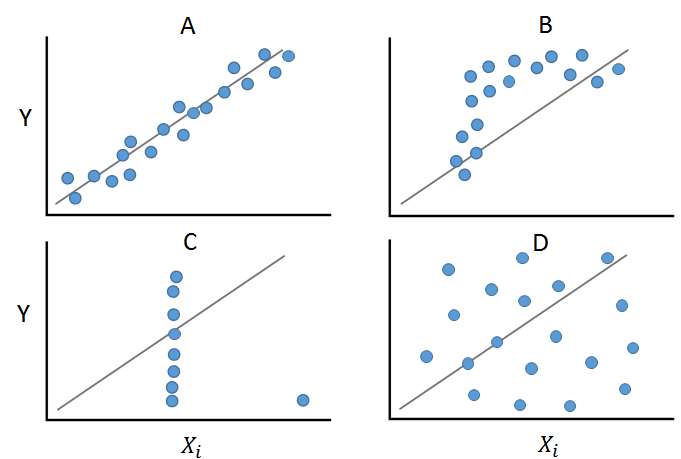
O Campo A mostra uma relação linear e monótona entre duas variáveis. Neste caso, a aplicação do cálculo do r de Pearson seria apropriada. O Campo B mostra uma relação monótona, mas não linear. Neste caso, o \(\rho\) de Spearman pode ser calculado. O Campo C mostra como um valor atípico pode alterar a estrutura da relação e, aqui, ambos os coeficientes de correlação dariam um valor distorcido. O Campo D mostra uma relação não linear e não monótona.
É evidente aqui que antes de calcular medidas, a análise gráfica é útil ou necessária!
Exemplo de Correlação
Agora você deve calcular a correlação entre Confiança no Parlamento (trstprl) e Confiança nos Políticos (trstplt) do PSS.
Ambas as variáveis são pseudo-métricas, portanto você deve calcular o r de Pearson.
Para isso, você precisa testar as suposições do r de Pearson:
Amostra de valores pareados \(\checkmark\)
ambas as variáveis são métricas \(\checkmark\)
relação entre as variáveis é linear
Verificação da Suposição
Você pode verificar isso facilmente criando um gráfico de dispersão. Para isso, você pode usar a função base plot(). No último bloco de aprendizado, conheceremos a biblioteca de gráficos mais poderosa ggplot2.
plot(
pss$trstprl,
pss$trstplt
)
Como os dados são apenas pseudo-métricos e muitos pontos de dados (inteiros) se sobrepõem, você pode não conseguir ver muito no gráfico.
Solução: Use a função jitter() para espalhar mais os pontos:
plot(
jitter(
pss$trstprl,
3
) ~
jitter(
pss$trstplt,
3
)
)
Esta análise gráfica requer um pouco de prática: Se você não ver padrões claros como no Quarteto de Anscombe, pode assumir uma relação linear.
Em conclusão, podemos afirmar que as condições são atendidas:
Amostra de valores pareados \(\checkmark\)
ambas as variáveis são métricas \(\checkmark\)
relação entre as variáveis é linear \(\checkmark\)
\(\Rightarrow\) Agora você pode calcular o r de Pearson!
Cálculo do Coeficiente
Para calcular o coeficiente de correlação, você usa a função cor() (tanto para o r de Pearson quanto para Spearman’s \(\rho\)). Primeiro, você precisa nomear as duas variáveis na função. Em seguida, você deve escolher o coeficiente de correlação e, por fim, escolher como lidar com NA's nas variáveis. Aqui, você exclui qualquer linha que tenha um valor NA em uma das duas variáveis.
cor(
pss$trstprl,
pss$trstplt,
method = "pearson", # alternativ hier "spearman"
use = "complete.obs"
) ## [1] 0.2318401A saída mostra um coeficiente de correlação de \(r \approx 0.232\). Nesta saída, não há valor de p incluído e você não pode fazer uma afirmação sobre a significância.
Calculando o coeficiente com a biblioteca psych
Com a biblioteca psych, você pode usar a função corr.test(), que também fornece o teste de significância:
install.packages("psych")
library("psych")corr.test(
pss$trstprl,
pss$trstplt,
method = "pearson",
use = "complete.obs"
) ## Call:corr.test(x = pss$trstprl, y = pss$trstplt, use = "complete.obs",
## method = "pearson")
## Correlation matrix
## [1] 0.23
## Sample Size
## [1] 4954
## These are the unadjusted probability values.
## The probability values adjusted for multiple tests are in the p.adj object.
## [1] 0
##
## To see confidence intervals of the correlations, print with the short=FALSE optionEste teste gera três matrizes (matriz de correlação, matriz de tamanho da amostra, matriz de valores de p), que você pode usar posteriormente para visualização.
A informação adicional necessária do valor de p está no último lugar. Aqui, temos um valor de p de \(0\).
Calculando várias correlações
Com ambas as funções, você pode calcular não apenas a correlação entre duas variáveis, mas também especificar mais de duas variáveis diretamente. Será calculada a correlação em pares entre todas as variáveis. Para isso, use a função c() para especificar entre quais variáveis você deseja obter valores de correlação em pares:
cor(
pss[
,
c(
"trstprl",
"trstplt",
"trstprt",
"trstlgl"
)
],
method = "pearson",
use = "complete.obs"
) ## trstprl trstplt trstprt trstlgl
## trstprl 1.0000000 0.22712300 0.3824902 0.22536686
## trstplt 0.2271230 1.00000000 0.3992831 0.05203906
## trstprt 0.3824902 0.39928307 1.0000000 0.24868786
## trstlgl 0.2253669 0.05203906 0.2486879 1.00000000corr.test(
pss[
,
c(
"trstprl",
"trstplt",
"trstprt",
"trstlgl"
)
],
method = "pearson",
use = "complete.obs"
) ## Call:corr.test(x = pss[, c("trstprl", "trstplt", "trstprt", "trstlgl")],
## use = "complete.obs", method = "pearson")
## Correlation matrix
## trstprl trstplt trstprt trstlgl
## trstprl 1.00 0.23 0.38 0.23
## trstplt 0.23 1.00 0.40 0.05
## trstprt 0.38 0.40 1.00 0.25
## trstlgl 0.23 0.05 0.25 1.00
## Sample Size
## trstprl trstplt trstprt trstlgl
## trstprl 4965 4954 4948 4953
## trstplt 4954 4989 4972 4977
## trstprt 4948 4972 4983 4971
## trstlgl 4953 4977 4971 4988
## Probability values (Entries above the diagonal are adjusted for multiple tests.)
## trstprl trstplt trstprt trstlgl
## trstprl 0 0 0 0
## trstplt 0 0 0 0
## trstprt 0 0 0 0
## trstlgl 0 0 0 0
##
## To see confidence intervals of the correlations, print with the short=FALSE optionAmbas as saídas mostram uma matriz de correlação. Os nomes das variáveis são fornecidos em cada coluna e linha. A diagonal é sempre \(1\), pois a relação entre a variável e ela mesma é \(1\) (ou seja, perfeita!).
Como podemos representar graficamente as correlações agora?