Fundamentos da Regressão Linear
Com uma regressão linear estimamos a relação causal entre uma (ou mais) variável independente e uma variável dependente. O modelo é geralmente estimado pelo método Ordinary-Least-Squares (OLS) e assim obtemos o melhor estimador linear (Best Linear Unbiased Estimator - BLUE). Isso é válido apenas se as suposições forem atendidas.
Com base em suposições teóricas ou evidências empíricas de outros pesquisadores (estado da arte), estimamos um modelo. As variáveis independentes são frequentemente divididas em variáveis de controle e variáveis sobre as quais queremos testar suposições teóricas.
O que deve ter sido retido das aulas de estatística?
Objetivo da regressão linear
Propriedades da regressão linear
Relações lineares
Matemática básica por trás da regressão linear
(Suposições de OLS)
Objetivos
Com a regressão linear, podemos responder às seguintes perguntas:
O modelo pode explicar a variância na variável dependente?
Quanto o modelo pode explicar?
O efeito da variável independente é significativo?
Em que direção o efeito da variável independente atua?
Quão forte é o efeito da variável independente (e quão forte é em relação a outras variáveis independentes)?
\(\Rightarrow\) Todas essas perguntas testam hipóteses formadas a partir do quadro teórico nas ciências sociais. Ou seja, antes da análise de dados, há uma teoria!
Características
As seguintes condições devem ser atendidas para calcular uma regressão linear:
\(\checkmark\) A variável dependente deve ser (pseudo-)métrica
\(\checkmark\) As variáveis independentes podem ser (pseudo-)métricas ou categóricas
\(\checkmark\) A relação entre cada variável independente e a variável dependente deve ser linear
Exemplo de regressão linear
Neste exemplo, usamos um conjunto de dados fictício estatísticas, que inclui, entre outras coisas, a nota da prova de Estatística I e a nota da prova de Estatística II dos alunos. Queremos calcular um modelo em que avaliamos o efeito da nota na prova de Estatística I (nota) na nota da prova de Estatística II (nota3).
Qual poderia ser nossa suposição teórica para isso?
Podemos testar uma relação linear por meio de um gráfico de dispersão. Como fazer isso, aprenderemos no último bloco de aprendizado!
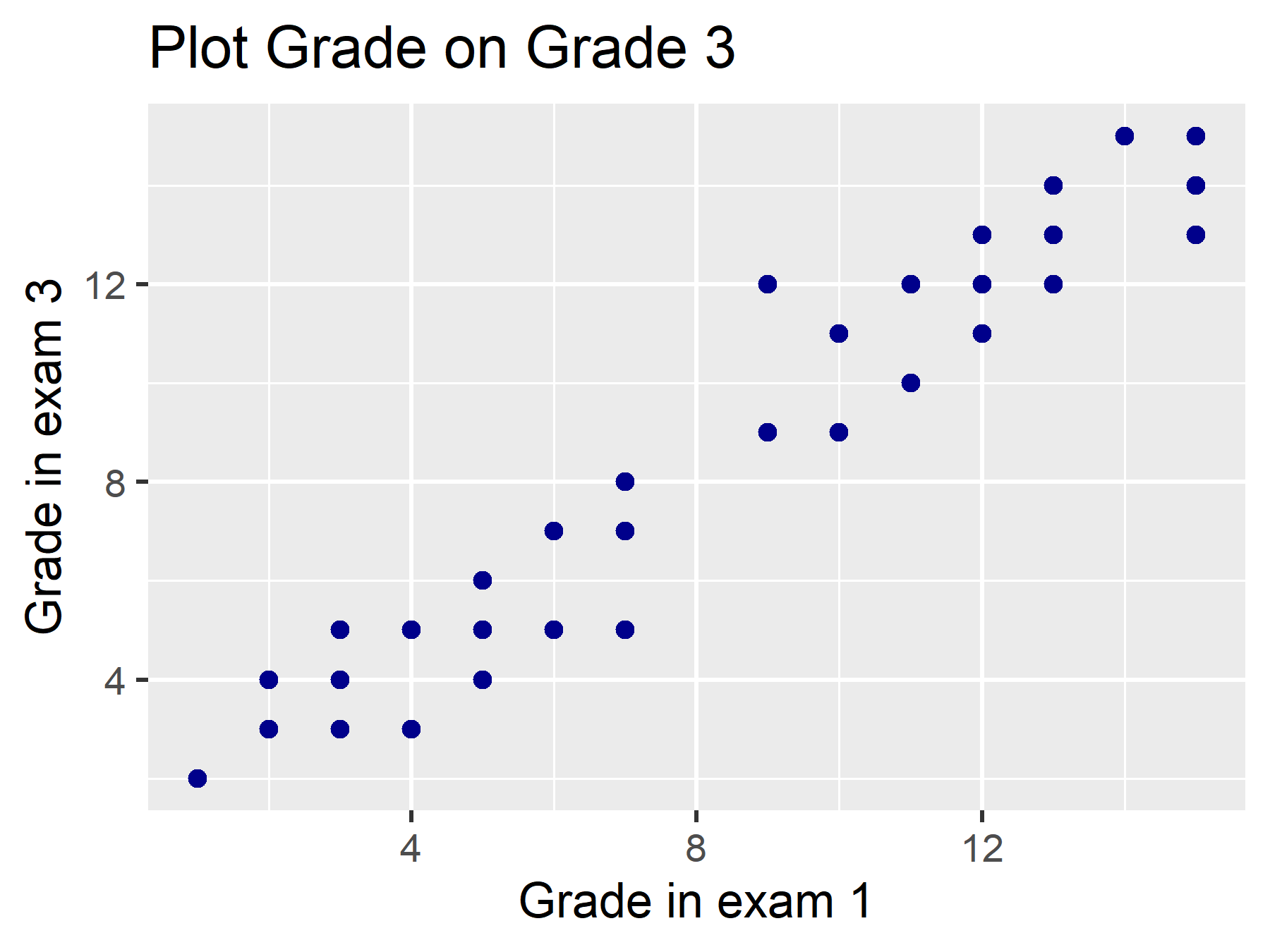
Matemática Básica
Em nosso exemplo, primeiro calculamos uma regressão linear bivariada:
variável dependente:
nota3(\(y\))variável independente:
nota(\(x_1\))
Portanto, a equação deste modelo de regressão (bivariado) é:
\(Y = \beta_0 + \beta_1 * X_1 + \varepsilon, \varepsilon \sim \mathcal{N}(0, \sigma^2)\)
\(Y\) é a variável dependente, \(X\) é a variável independente e \(\varepsilon\) representa os resíduos.
O que é novamente \(\varepsilon\)?
E o que significa essa expressão \(\varepsilon \sim \mathcal{N}(0, \sigma^2)\) novamente?
\(\varepsilon\) inclui os resíduos. Estes são as distâncias entre o valor estimado (\(\hat{y}\), pontos verdes) e o valor observado (\(y\), pontos azuis).
\(\varepsilon \sim \mathcal{N}(0, \sigma^2)\) significa que esses erros são distribuídos normalmente. Algumas distâncias são positivas, outras negativas. No entanto, no total, elas têm média de \(0\) e variância de \(\sigma^2\).
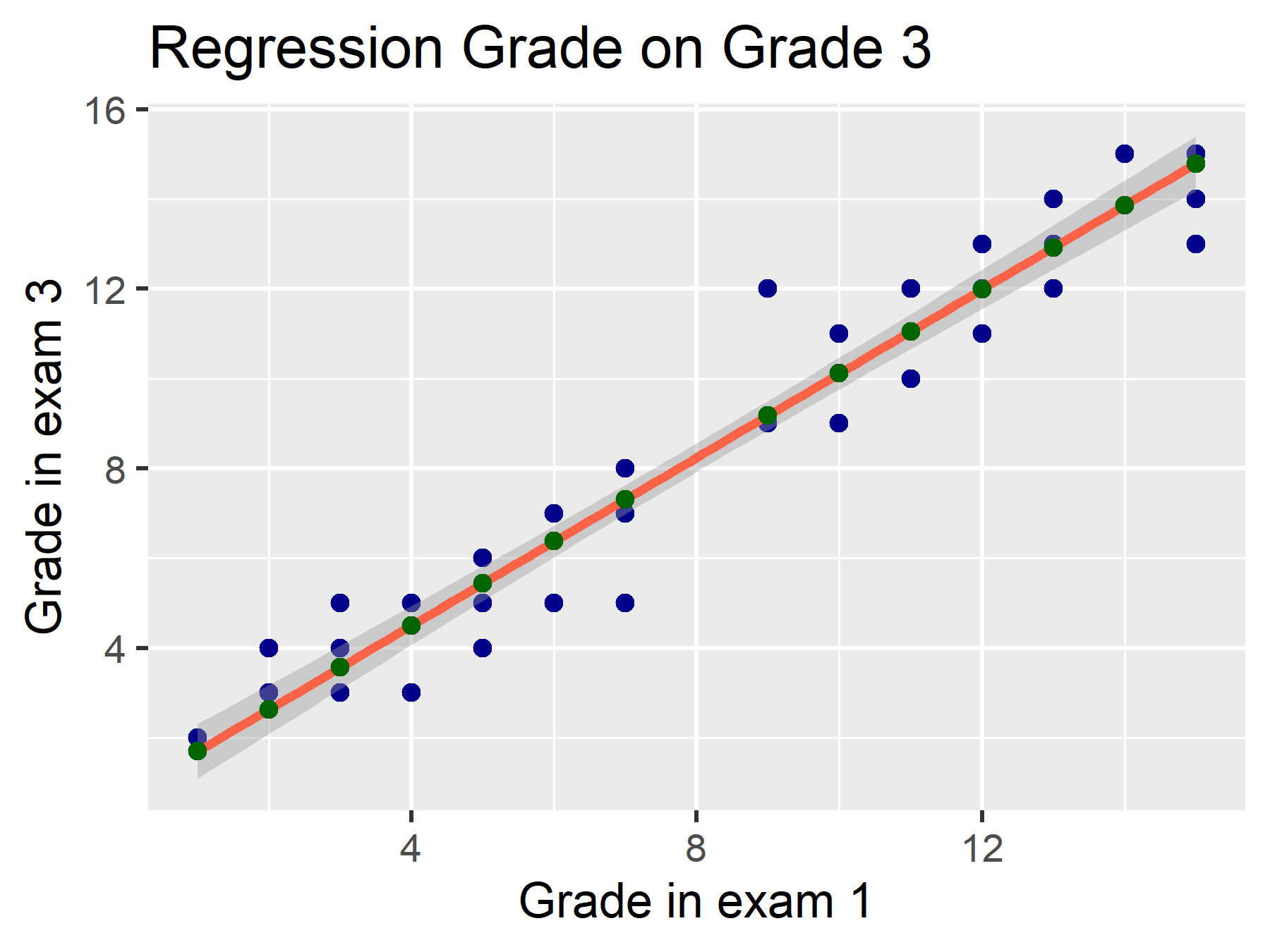
Equação da Regressão Linear
Vamos recapitular a equação da regressão linear:
\(Y = \beta_0 + \beta_1*X_1 + \varepsilon\)
Também podemos escrever a equação para cada caso, com um índice de execução i:
\(y_i = \beta_0 + \beta_1 * {x_1}_i + \epsilon_i\)
As Regressões Lineares são calculadas por padrão com o método de Mínimos Quadrados Ordinários (OLS). O que isso significa novamente?
\(\sum_{i=1}^n(\hat{y_i} - y_i)^2 \to min.\)
\(\Rightarrow\) O modelo escolhe a linha que minimiza a soma dos quadrados das distâncias.
Também podemos usar Álgebra de Matrizes para representar isso. Isso ajuda (alguns) a entender melhor em R, já que trabalhamos com vetores, matrizes e data frames (como uma forma especial de matriz):
\(Y = X\beta + E\)
\(\begin{bmatrix}y_1 \\y_2 \\... \\y_n \\\end{bmatrix} = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ 1 & ...\\ 1 & x_n\\ \end{bmatrix} \begin{bmatrix}\beta_0 \\ \beta_1\\\end{bmatrix} + \begin{bmatrix}\epsilon_1 \\ \epsilon_2 \\ ... \\ \epsilon_n \\ \end{bmatrix}\)
O modelo calcula a matriz \(\beta\) - no caso bivariado, dois coeficientes: Interceptação (intercept) e Inclinação (slope) da variável independente. Como resultado do cálculo dos coeficientes, obtemos \(E\) (Resíduo, Diferença em relação aos valores observados).
Na próxima página, vamos ver um exemplo concreto!