Unidade 4 > Regressão Linear > Regressão Linear Bivariada

Regressão Linear Bivariada

Estamos utilizando novamente o conjunto de dados PSS, que tem sido usado ao longo de todo o exercício. Agora queremos testar até que ponto a satisfação com o desempenho econômico explica a satisfação com a democracia. As duas variáveis necessárias para esta regressão linear são stfeco e stfdem. A premissa teórica por trás disso é que as pessoas que estão satisfeitas economicamente também estão mais satisfeitas com o sistema político como um todo.

Como seria a equação para este caso?

Seria possível calcular um modelo que explique a satisfação com o desempenho econômico pela satisfação com a democracia?

Sim, é possível! No entanto, você teria que alterar as suposições teóricas aqui. Você vê que os modelos estatísticos não são autônomos, mas sempre têm um ponto de referência teórico!

Cálculo do Exemplo

No R, usamos a função lm() para calcular um modelo de regressão linear. É importante conhecer a fórmula, pois a especificamos como uma fórmula na função.

Nós armazenamos o resultado do cálculo do modelo em um objeto! No argumento da função lm(), você fornece a fórmula da regressão linear como primeiro argumento e o objeto de dados como segundo argumento, neste caso pss. O conjunto de dados está disponível no projeto do RStudio na pasta data. Se estiver trabalhando com uma versão local, você pode baixar o conjunto de dados aqui:

Conjunto de Dados

.DS_Store (6 KB)

PSS_Codebook.pdf (94 KB)

pss.rds (63 KB)

olsModel <- lm(
  stfdem ~ 1 + stfeco, #Formel der Regression
  data = pss # Datenobjekt
)

No modelo, obtemos diferentes valores que precisamos interpretar: Coeficientes, valor-t (ou pr(>|t|)) e (ajustado) R².

As seguintes perguntas devem ser respondidas no final de cada modelo:

Quanto o modelo consegue explicar?
Quais efeitos têm as variáveis individuais?

Os valores individuais são interpretados passo a passo. Os resultados são chamados com a função summary():

summary(olsModel)

## 
## Call:
## lm(formula = stfdem ~ 1 + stfeco, data = pss)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.7171 -1.0990  0.0283  1.1556  5.7737 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.48085    0.06939    6.93 4.75e-12 ***
## stfeco       0.87271    0.01354   64.44  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.733 on 4902 degrees of freedom
##   (96 observations deleted due to missingness)
## Multiple R-squared:  0.4587,	Adjusted R-squared:  0.4585 
## F-statistic:  4153 on 1 and 4902 DF,  p-value: < 2.2e-16

Interpretação dos Coeficientes

coef(olsModel)

## (Intercept)      stfeco 
##   0.4808475   0.8727124

Como interpretamos o valor para stfeco?

$\Rightarrow$ Com cada aumento de uma unidade em stfeco, stfdem também aumenta em $0.8727124$ pontos.

$\Rightarrow$ Uma pessoa com o valor $0$ em stfeco atinge o valor $0.4808475emstfdem` (Intercept).

Com a função confint(), obtemos os intervalos estimados (em summary() obtemos apenas o valor-t e valor-p):

confint(olsModel)

##                 2.5 %    97.5 %
## (Intercept) 0.3448187 0.6168763
## stfeco      0.8461641 0.8992608

Nas ciências sociais, a interpretação do Intercept na maioria dos casos é menos relevante. Portanto, focamos principalmente na influência de grade. O intervalo de confiança vai de $[0.8461641, 0.8992608]$ e não inclui o valor $0. Portanto, esse efeito é significativo. Rejeitamos a hipótese nula de que esse efeito é igual a $0 ($_1 =0`).

Intervalos de Confiança e Valor de p

O que nos dizem o intervalo de confiança e o valor de p?

Calculamos o efeito médio de stfeco em stfdem e o intervalo de confiança desse efeito.
Com testes de significância (na maioria dos casos, testes t), concluímos que o valor populacional ($\mu$) desse cálculo não é igual a $0$ (valor de p significativo): É então muito improvável ($95 %$) que $\mu = 0$.
O valor de p não nos permite dizer que o valor real corresponde ao valor calculado (por exemplo, com $95 %$ de confiança, a verdadeira média está dentro do intervalo de confiança calculado). Pois não sabemos se nossa amostra é uma das amostras que incluem o valor verdadeiro ($\mu$) ($95 %$ das amostras incluem o valor).
Valores não significativos nos dizem, portanto, que não podemos excluir que o verdadeiro valor populacional ($\mu$) seja igual a $0$; mas não podemos dizer que o valor verdadeiro é igual a $0$.

$\Rightarrow$ Confuso? Apenas lembre-se de que se trata de falsificação e não de verificação (base da pesquisa social empírica!).

Outras Possibilidades de Saída

Se tivermos a computação armazenada em um objeto, podemos acessar diferentes partes do modelo (por exemplo, coeficientes, valores estimados ou resíduos):

olsModel$coefficients # Koeffizienten

## (Intercept)      stfeco 
##   0.4808475   0.8727124

head(olsModel$fitted.values) # geschätzte Werte

##        1        2        3        4        5        6 
## 5.717122 6.589834 5.717122 3.971697 4.844410 5.717122

head(olsModel$residuals) # Residuen

##          1          2          3          4          5          6 
##  1.2828780  1.4101656  0.2828780  1.0283029 -0.8444096  0.2828780

Também podemos usar as seguintes funções em vez disso: coef(), fitted(), resid() ou confint().

coef(olsModel) # Koeffizienten

## (Intercept)      stfeco 
##   0.4808475   0.8727124

head(fitted(olsModel)) # ersten 6 geschätzten Werte

##        1        2        3        4        5        6 
## 5.717122 6.589834 5.717122 3.971697 4.844410 5.717122

head(resid(olsModel)) # Residuen

##          1          2          3          4          5          6 
##  1.2828780  1.4101656  0.2828780  1.0283029 -0.8444096  0.2828780

confint(olsModel) # Konfidenzintervalle

##                 2.5 %    97.5 %
## (Intercept) 0.3448187 0.6168763
## stfeco      0.8461641 0.8992608

Avaliação Global do Modelo

Para avaliar globalmente a qualidade do modelo, muitas vezes é fornecido o coeficiente de determinação $R^2$. $R^2$ fornece a informação sobre quanto da variância da variável dependente pode ser explicada pelo modelo.

A equação é a seguinte:

\[R^2 = \frac{\sum_{i=1}^n(\hat{y_i}-\bar{y})^2}{\sum_{i=1}^n(y_i-\bar{y})^2} = \frac{variância \, explicada}{variância \, total}\]

$R^2$

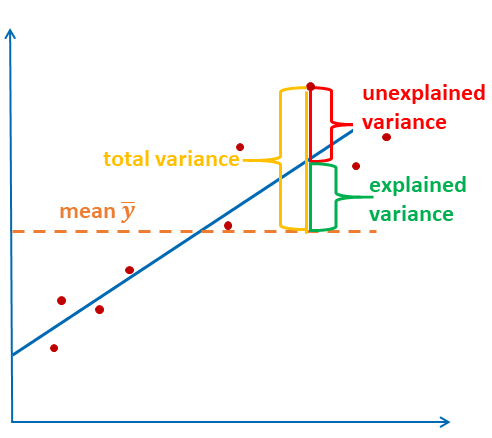
O gráfico representa a fórmula novamente: a variância explicada é a soma dos quadrados das distâncias entre o valor estimado e a média. A variância total é a soma dos quadrados das distâncias entre o valor observado e a média.

Como descrevemos agora o resultado? $R^2$ é fornecido na penúltima linha.

summary(olsModel)

## 
## Call:
## lm(formula = stfdem ~ 1 + stfeco, data = pss)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.7171 -1.0990  0.0283  1.1556  5.7737 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.48085    0.06939    6.93 4.75e-12 ***
## stfeco       0.87271    0.01354   64.44  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.733 on 4902 degrees of freedom
##   (96 observations deleted due to missingness)
## Multiple R-squared:  0.4587,	Adjusted R-squared:  0.4585 
## F-statistic:  4153 on 1 and 4902 DF,  p-value: < 2.2e-16

O modelo explica $45.85 %$ da variância da satisfação com a democracia (stfdem) ($R^2$). Uma maior satisfação com o desempenho econômico (stfeco) está positivamente relacionada com a satisfação com a democracia (stfdem). Para cada aumento de uma unidade na satisfação com o desempenho econômico, o valor da satisfação com a democracia aumenta em $0.87271$. O efeito de stfeco em stfdem é significativo ($p<0.001$).