Grundlagen der linearen Regression
Mit einer linearen Regression schätzen wir die kausale Beziehung zwischen mehreren unabhängigen Variablen und einer abhängigen Variable. Das Modell wird i.d.R. mit dem Verfahren Ordinary-Least-Squares (OLS) geschätzt und so erhalten wir den besten linearen Schätzer (Best Linear Unbiased Estimator - BLUE). Dies gilt aber nur sofern die Annahmen der linearen Regression zutreffen.
Basierend auf theoretischen Annahmen oder empirischer Evidenz anderer Forscher:innen (state of the art) schätzen wir ein Modell. Die unabhängigen Variablen werden oftmals geteilt in Kontrollvariablen und Variablen, über die wir theoretische Annahmen testen möchten.
Was solltest du dir aus den Statistik-Vorlesungen in Erinnerung rufen, bevor du im Lernmodul weitergehst?
Was ist eine lineare Beziehung?
Was ist das Ziel der linearen Regression?
Welche Eigenschaften müssen für eine lineare Regression erfüllt sein?
Wie verstehe ich die Gleichung einer linearen Regression?
(Was sind die Annahmen der Schätzung (OLS)?)
Was ist eine lineare Beziehung?
In diesem Beispiel nutzen wir wieder den Datensatz PSS, der unter anderem die Zufriedenheit mit der Demokratie (stfdem) und die Zufriedenheit mit der Wirtschaft (stfeco) enthält. Wir möchten ein Modell berechnen, in dem wir einen Effekt Zufriedenheit mit der Wirtschaft auf die Demokratiezufriedenheit berechnen. Wir schätzen also, inwieweit die Zufriedenheit mit der Wirtschaft die Demokratiezufriedenheit beeinflusst.
Überlege kurz, was dafür unsere theoretische Annahme sein könnte.
Eine lineare Beziehung können wir über ein Scatterplot testen.
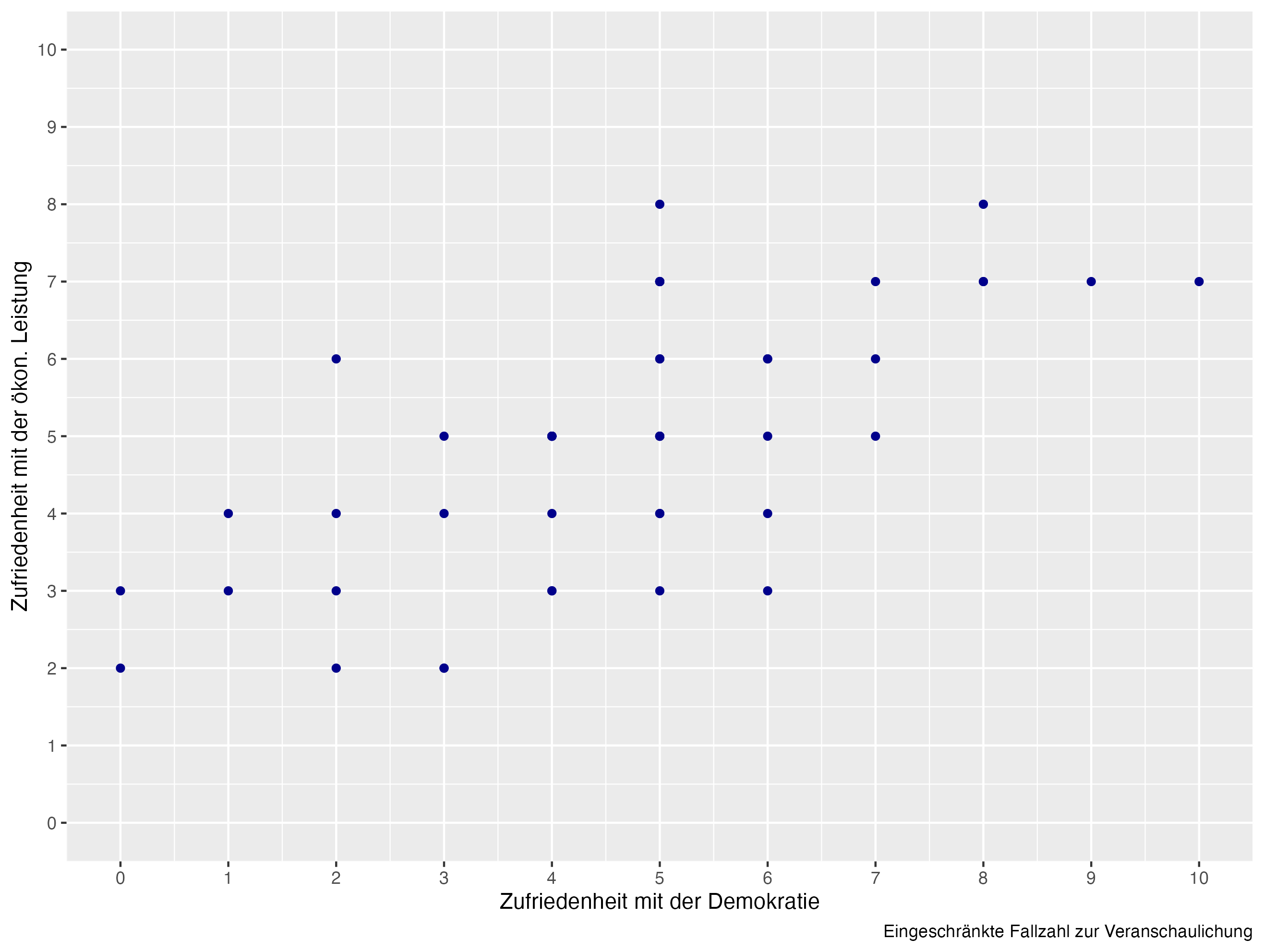
Was ist das Ziel der linearen Regression?
Mit der linearen Regression können wir folgende Fragen beantworten:
Kann das Modell Varianz in der abhängigen Variable erklären?
Wie viel kann das Modell erklären?
Ist der Effekt der unabhängigen Variable signifikant?
In welche Richtung wirkt der Effekt der unabhängigen Variable?
Wie stark ist der Effekt der unabhängigen Variable (und wie stark ist er in Relation zu weiteren unabhängigen Variablen)?
\(\Rightarrow\) Mit all diesen Fragen werden in den Sozialwissenschaften gebildete Hypothesen aus der Theorie getestet. Das heißt vor der Datenanalyse steht eine Theorie!
Welche Eigenschaften müssen für eine lineare Regression erfüllt sein?
Folgende Bedingungen müssen vorliegen, um eine lineare Regression berechnen zu können:
\(\checkmark\) abhängige Variable muss (pseudo-)metrisch sein
\(\checkmark\) unabhängige Variablen können (pseudo-)metrisch oder kategorial sein
\(\checkmark\) die Beziehung zwischen jeder unabhängigen Variable und der abhängigen Variable muss linear sein
Wie verstehe ich die Gleichung einer linearen Regression?
Wir berechnen in unserem Beispiel zuerst eine bivariate lineare Regression, damit du das Grundmodell besser verstehen kannst:
abhängige Variable:
stfdem(\(y\), Zufriedenheit mit der Demokratie)unabhängige Variable:
stfeco(\(x_1\), Zufriedenheit mit der Wirtschaft)
Die Gleichung dieses (bivariaten) Regressionsmodells lautet daher:
\(Y = \beta_0 + \beta_1 * X_1 + \varepsilon, \varepsilon \sim \mathcal{N}(0, \sigma^2)\)
\(Y\) ist die unabhängige Variable, \(X\) die abhängige Variable und \(\varepsilon\) stellt die Residuen (Schätzfehler) dar.
Was ist nochmal \(\varepsilon\)?
Und was bedeutet dieser Ausdruck \(\varepsilon \sim \mathcal{N}(0, \sigma^2)\) nochmal?
\(\varepsilon\) umfasst die Residuen. Dies sind die Abstände zwischen geschätztem Wert (\(\hat{y}\), grüne Punkte) und beobachtetem Wert (\(y\), blaue Punkte).
\(\varepsilon \sim \mathcal{N}(0, \sigma^2)\) bedeutet, dass diese Fehler normalverteilt sind. Manche Abstände sind positiv, andere negativ. In Summe haben diese aber den Mittelwert \(0\) und die Varianz \(\sigma^2\).
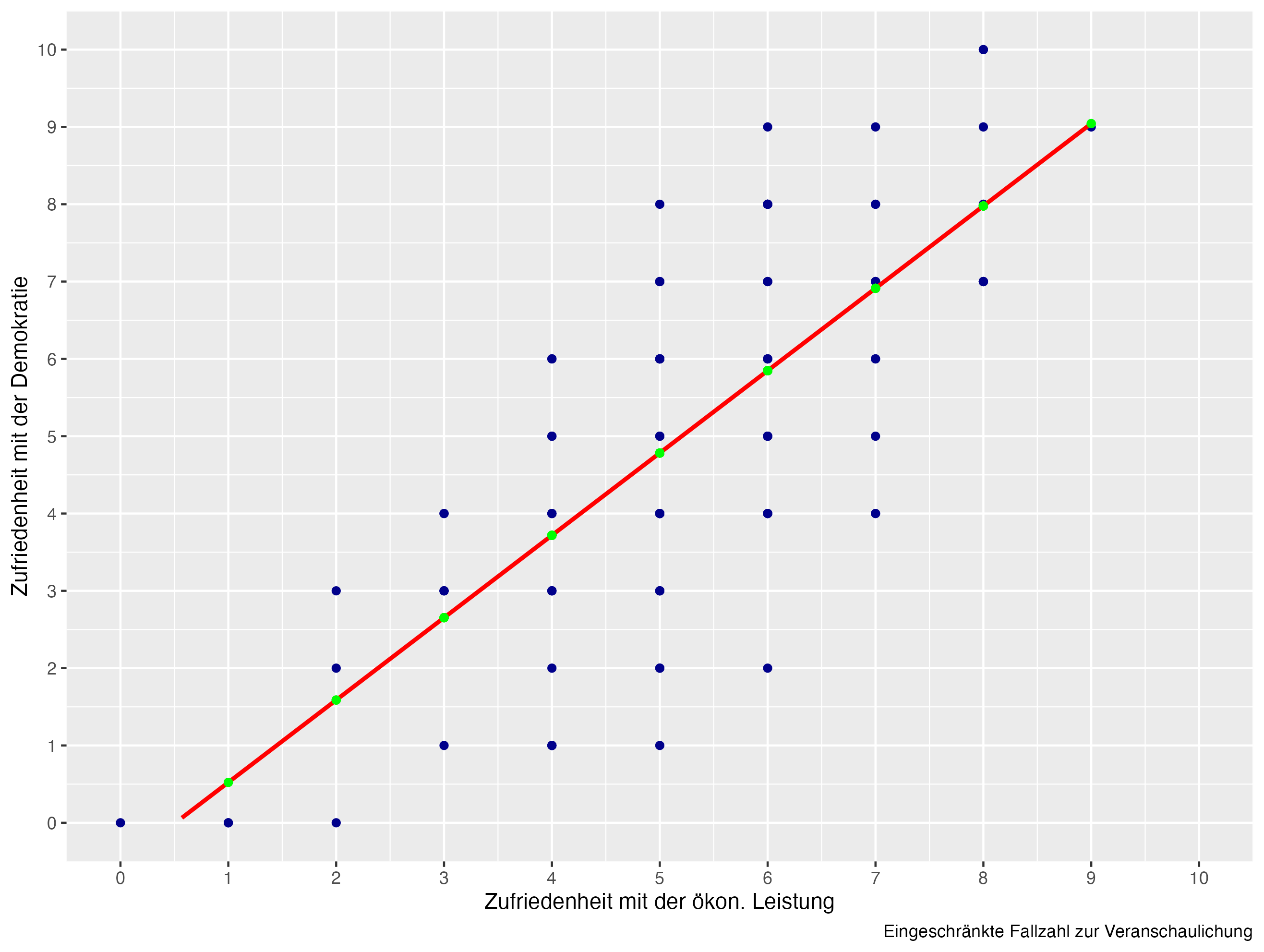
Wiederholen wir kurz die Gleichung der linearen Regression:
\(Y = \beta_0 + \beta_1*X_1 + \varepsilon\)
Wir können die Gleichung auch für jeden Fall aufstellen, mit einem Laufindex i:
\(y_i = \beta_0 + \beta_1 * {x_1}_i + \epsilon_i\)
Was sind die Annahmen der Schätzung (OLS)?
Lineare Regressionen werden standardmäßig mit dem Ordinary-Least-Squared-Verfahren (OLS) berechnet. Was heißt das nochmal?
\(\sum_{i=1}^n(\hat{y_i} - y_i)^2 \to min.\)
\(\Rightarrow\) Das Modell wählt die Linie, die die summierten quadrierten Abstände minimiert.
Wir können für die Darstellung auch Matrix-Algebra nutzen. Dies hilft (manchen) es besser zu verstehen:
\(Y = X\beta + E\)
\(\begin{bmatrix}y_1 \\y_2 \\... \\y_n \\\end{bmatrix} = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ 1 & ...\\ 1 & x_n\\ \end{bmatrix} \begin{bmatrix}\beta_0 \\ \beta_1\\\end{bmatrix} + \begin{bmatrix}\epsilon_1 \\ \epsilon_2 \\ ... \\ \epsilon_n \\ \end{bmatrix}\)
Das Modell berechnet die Matrix \(\beta\) - im bivariaten Fall zwei Koeffizienten: Konstante (intercept, \(\beta_0\)) und Steigung (slope, \(\beta_1\)) der unabhängigen Variable. Als Ergebnis der Berechnung der Koeffizienten ergibt sich \(E\) (Residuum, Differenz zu beobachteten Werten).
Auf der nächsten Seite schauen wir uns ein konkretes Beispiel an und du wirst sehen, es ist nicht schwer nachzuvollziehen!