Bivariate lineare Regression

Berechnung des Beispiels

Die Berechnung der linearen Regression kann über die Syntax oder Klickwege leicht berechnet werden.

Klickweg Syntax Ergebnis

REGRESSION
/MISSING LISTWISE 
/STATISTICS COEFF CI(.95) R ANOVA 
/NOORIGIN
/DEPENDENT stfdem
/METHOD=ENTER stfeco.

Aufgerufen wird die lineare Regression mit dem Hauptbefehl REGRESSION. Mit dem Unterbefehl /MISSING LISTWISE weisen wir an, dass fehlende Werte listenweise ausgeschlossen werden. Unter /STATISTICS geben wir an, was uns SPSS ausgeben soll: Hier die Koeffizienten, deren Konfidenzintervalle, \(R^2\) sowie die ANOVA. Unter /DEPENDENT geben wir die abhängige Variable, hier also stfdem an. Danach folgen unter /METHOD=ENTER die abhängige(n) Variable(n), in unserem Beispiel nur stfeco.

Das war’s auch schon für die Syntax!

Hier siehst du nun die einzelnen Ausgaben, die wir mit dem Befehl angefordert haben. Im nächsten Schritt gehen wir diese Ausgabe einzeln durch.

Folgende Fragen sollten am Ende zu jedem Modell beantwortet werden:

• Wie viel kann das Modell erklären?

• Welche Effekte haben die einzelnen Variablen?

Die einzelnen Werte werden nun Schritt für Schritt interpretiert.

Interpretation der Koeffizienten

Zuerst schauen wir uns den Koeffizientenblock an, in dem die einzelnen Werte der Regression ausgegeben werden.

Koeffizientenblock

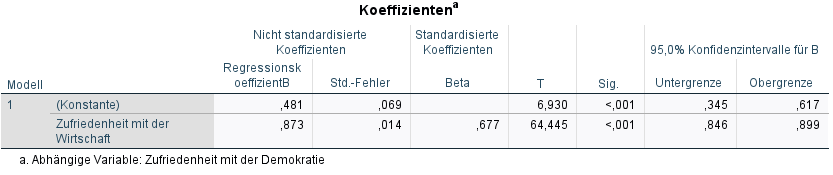
Dazu schaust du dir in der Ausgabe den Koeffizientenblock an. Hierin sind alle Variablen aufgeführt, die wir per Befehl bzw. aus der Formel zum Modell hinzugefügt haben. Hier also die Konstante (Intercept, \(\beta_0\)) und der Regressionskoeffizient für die Zufriedenheit mit der Wirtschaft (stfeco, \(\beta_2\)).

In den Spalten siehst du das SPSS sowohl den nicht standardisierten Koeffizient und dessen Standardfehler und auch den standardisierten Koeffizienten ausgibt. In den Statistik-Vorlesungen hast du ja bereits die z-Standardisierung kennengelernt um Verteilungen von Variablen besser vergleichen zu können. Die z-Standardisierung rekodiert eine Variable auf die Einheit Standardabweichung, so dass Variablen, die z-standardisiert sind, vergleichbar sind.

In den anschließenden Spalten siehst du noch den Signifikanzwert, wobei hier der t-Wert sowie die Signifikanz mit dem p-Wert angegeben wird. Es ist also für dich direkt lesbar, ob ein Effekt signifikant ist oder nicht (p-Wert \(< 0.05\)).

Zuletzt siehst du noch das angegebene Konfidenzintervall für die nicht standardisierten Koeffizienten.

In den Sozialwissenschaften ist die Interpretation des Intercepts in den meisten Fällen weniger relevant. Deshalb schauen wir primär auf den Einfluss von stfeco.

Wie interpretieren wir den Wert für stfeco?

\(\Rightarrow\) Mit jedem Anstieg um eine Einheit in stfeco, steigt auch stfdem um \(0.873\) Punkte auf der Skala (nicht standardisierter Regressionskoeffizient).

\(\Rightarrow\) Eine Person, die den Wert \(0\) in stfeco hat, erreicht den Wert \(0.481\) in stfdem (Intercept, nicht standardisierter Regressionskoeffizient).

Der standardisierte Regressionskoeffizient zeigt die Steigung der Demokratiezufriedenheit in Standardabweichungen an. Dies ist insbesondere für multivariate Modelle relevant, da nur die standardisierten Regressionskoeffizienten von Variablen mit verschiedenen Skalen hinsichtlich der Stärke des Einflusses verglichen werden können. In unserem Beispiel steigt also die Demokratiezufriedenheit um 0.014 Standardabweichungen, wenn die Zufriedenheit mit der Wirtschaft um eine Standardabweichung erhöht wird.

Das Konfidenzintervall geht von \([0.846, 0.899]\) und inkludiert nicht den Wert \(0\). Dieser Effekt ist daher signifikant. Wir verwerfen die Nullhypothese, dass dieser Effekt gleich \(0\) ist (\(\beta_1 = 0\)).

Globale Bewertung des Modells

Zur globalen Bewertung der Modellgüte wird oftmals das Bestimmtheitsmaß \(R^2\) angegeben. \(R^2\) liefert die Information, wie viel der Varianz der abhängigen Variablen durch das Modell erklärt werden kann.

Die Gleichung lautet:

\[R^2 = \frac{\sum_{i=1}^n(\hat{y_i}-\bar{y})^2}{\sum_{i=1}^n(y_i-\bar{y})^2} = \frac{erklärte \, Varianz}{gesamte \, Varianz}\]

\(R^2\)

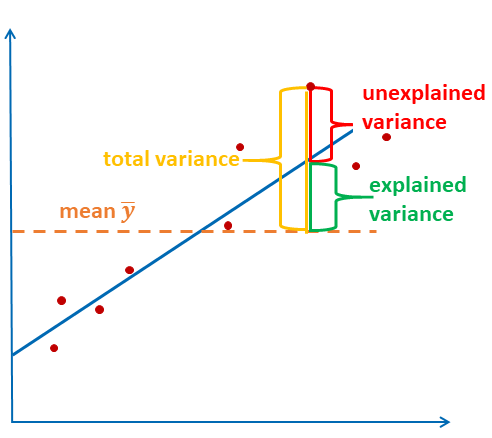
Die Grafik stellt die Formel nochmal dar: die erklärte Varianz ist die Summe der quadrierte Abstände zwischen geschätztem Wert und dem Mittelwert. Die gesamte Varianz ist die Summe der quadrierten Abstände zwischen beobachtetem Wert und dem Mittelwert.

In SPSS schauen wir dazu in die Modellzusammenfassung:

Modellzusammenfassung

Wir sehen angegeben \(R\), \(R^2\) sowie ein korrigiertes \(R^2\). Das korrigierte \(R^2\) wird für Modelle genutzt, in dem mehr als eine unabhängige Variable eingefügt wurde, da sich \(R^2\) durch das Hinzufügen einzelner Variablen erhöht und daher korrigiert werden muss. Da wir in der Regel multivariate Modelle berechnen und dieses bivariate Modell nur zur Veranschaulichung dient, schauen wir uns deshalb auch hier direkt das korrigierte \(R^2\) an. Der Wert liegt bei \(R^2 = 0.459\). Was sagt uns das nun?

So und jetzt gehen wir weiter und fügen weitere Variablen in das Modell hinzu!