Bivariate lineare Regression

Berechnung des Beispiels

In R nutzen wir die Funktion lm() um ein lineares Regressionsmodell zu berechnen. Es ist wichtig die Formel zu kennen, da wir das Modell als Formel in der Funktion angeben.

Wir speichern das Ergebnis der Modellberechnung in einem Objekt! In der Funktion lm() gibst du im ersten Argument die Formel der linearen Regression an und im zweiten Argument gibst du das Datenobjekt an, in diesem Fall pss. Der Datensatz ist im RStudio Projekt im Ordner data vorhanden. Falls du mit einer lokalen Version arbeitest, kannst du den Datensatz hier herunterladen:

olsModel <- lm(
  stfdem ~ 1 + stfeco, #Formel der Regression
  data = pss # Datenobjekt
)  

Wir erhalten im Modell verschiedene Werte, die wir interpretieren müssen: Coefficients, t-value(or pr(>|t|)) und (adjusted) R-Squared.

Folgende Fragen sollten am Ende zu jedem Modell beantwortet werden:

• Wie viel kann das Modell erklären?

• Welche Effekte haben die einzelnen Variablen?

Die einzelnen Werte werden nun Schritt für Schritt interpretiert. Die Ergebnisse werden mit der Funktion summary() aufgerufen:

summary(olsModel) 

## 
## Call:
## lm(formula = stfdem ~ 1 + stfeco, data = pss)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.7171 -1.0990  0.0283  1.1556  5.7737 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.48085    0.06939    6.93 4.75e-12 ***
## stfeco       0.87271    0.01354   64.44  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.733 on 4902 degrees of freedom
##   (96 observations deleted due to missingness)
## Multiple R-squared:  0.4587,	Adjusted R-squared:  0.4585 
## F-statistic:  4153 on 1 and 4902 DF,  p-value: < 2.2e-16

Interpretation der Koeffizienten

coef(olsModel)

## (Intercept)      stfeco 
##   0.4808475   0.8727124

Wie interpretieren wir den Wert für stfeco?

\(\Rightarrow\) Mit jedem Anstieg um eine Einheit in stfeco, steigt auch stfdem um \(0.8727124\) Punkte.

\(\Rightarrow\) Eine Person, die den Wert \(0\) in stfeco hat, erreicht den Wert \(0.4808475\) in stfdem (Intercept).

Mit der Funktion confint() erhalten wir die geschätzten Intervalle (in summary() erhalten wir nur den t-value und p-value):

confint(olsModel)

##                 2.5 %    97.5 %
## (Intercept) 0.3448187 0.6168763
## stfeco      0.8461641 0.8992608

In den Sozialwissenschaften ist die Interpretation des Intercepts in den meisten Fällen weniger relevant. Deshalb schauen wir primär auf den Einfluss von grade. Das Konfidenzintervall geht von \([0.8461641, 0.8992608]\) und inkludiert nicht den Wert \(0\). Dieser Effekt ist daher signifikant. Wir verwerfen die Nullhypothese, dass dieser Effekt gleich \(0\) ist (\(\beta_1 =0\)).

olsModel$coefficients # Koeffizienten

## (Intercept)      stfeco 
##   0.4808475   0.8727124

head(olsModel$fitted.values) # geschätzte Werte

##        1        2        3        4        5        6 
## 5.717122 6.589834 5.717122 3.971697 4.844410 5.717122

head(olsModel$residuals) # Residuen

##          1          2          3          4          5          6 
##  1.2828780  1.4101656  0.2828780  1.0283029 -0.8444096  0.2828780

coef(olsModel) # Koeffizienten

## (Intercept)      stfeco 
##   0.4808475   0.8727124

head(fitted(olsModel)) # ersten 6 geschätzten Werte

##        1        2        3        4        5        6 
## 5.717122 6.589834 5.717122 3.971697 4.844410 5.717122

head(resid(olsModel)) # Residuen

##          1          2          3          4          5          6 
##  1.2828780  1.4101656  0.2828780  1.0283029 -0.8444096  0.2828780

confint(olsModel) # Konfidenzintervalle

##                 2.5 %    97.5 %
## (Intercept) 0.3448187 0.6168763
## stfeco      0.8461641 0.8992608

Globale Bewertung des Modells

Zur globalen Bewertung der Modellgüte wird oftmals das Bestimmtheitsmaß \(R^2\) angegeben. \(R^2\) liefert die Information, wie viel der Varianz der abhängigen Variablen durch das Modell erklärt werden kann.

Die Gleichung lautet:

\[R^2 = \frac{\sum_{i=1}^n(\hat{y_i}-\bar{y})^2}{\sum_{i=1}^n(y_i-\bar{y})^2} = \frac{erklärte \, Varianz}{gesamte \, Varianz}\]

\(R^2\)

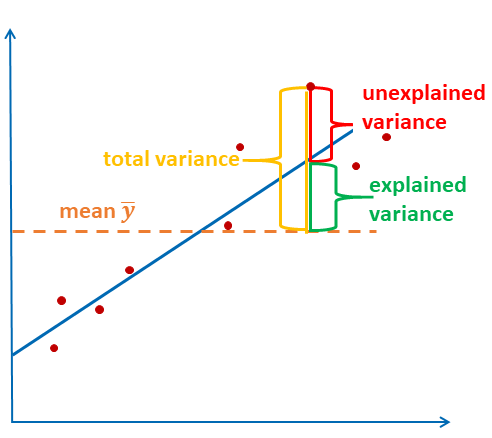
Die Grafik stellt die Formel nochmal dar: die erklärte Varianz ist die Summe der quadrierte Abstände zwischen geschätztem Wert und dem Mittelwert. Die gesamte Varianz ist die Summe der quadrierten Abstände zwischen beobachtetem Wert und dem Mittelwert.

summary(olsModel)

## 
## Call:
## lm(formula = stfdem ~ 1 + stfeco, data = pss)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.7171 -1.0990  0.0283  1.1556  5.7737 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.48085    0.06939    6.93 4.75e-12 ***
## stfeco       0.87271    0.01354   64.44  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.733 on 4902 degrees of freedom
##   (96 observations deleted due to missingness)
## Multiple R-squared:  0.4587,	Adjusted R-squared:  0.4585 
## F-statistic:  4153 on 1 and 4902 DF,  p-value: < 2.2e-16