metrische Variable
Darstellung Histogramm mit Normalverteilungskurve
Ein Histogramm setzt auf der X-Achse gleichbleibende Abstände voraus. Daher ist es zu empfehlen, hier Variablen mit metrischem Skalenniveau zu verwenden. Daher kannst du hier nicht wie beim Säulendiagramm die Reihenfolge der Balken mit /FORMATS frei bestimmen.
FREQUENCIES VARIABLES=wkhtot
/HISTOGRAM NORMAL
/ORDER=ANALYSIS.
Auch hier kannst du mit FREQUENCIES arbeiten. Neu ist der Unterbefehl /HISTOGRAM. Wenn du magst, kannst du dir dazu eine Normalverteilungskurve mit dem Parameter NORMAL ausgeben lassen. Was war das nochmal? Schau unten nach.
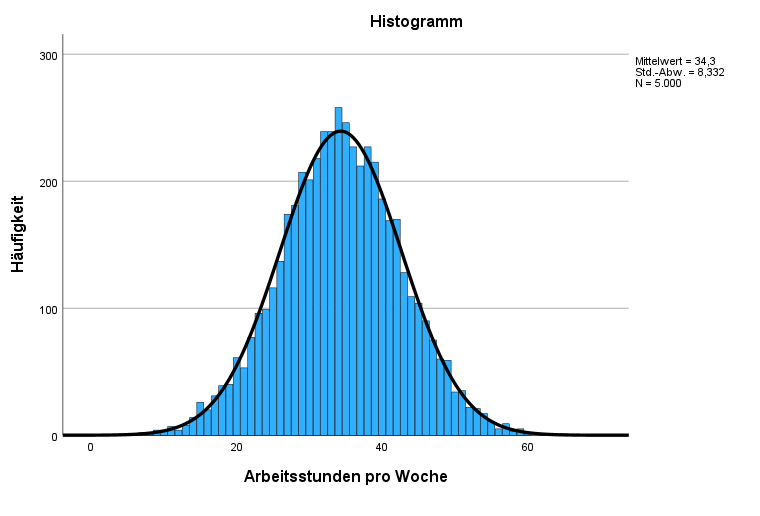
Hier sehen wir nun also, dass die erhobene Variable nahezu perfekt einer Normalverteilung gleicht. Dies ist wichtig für spätere bi- und multivariate Verfahren. Denn die Normalverteilung ist oftmals Voraussetzung für solche Verfahren.
Exkurs I graphische Diagnose, Schiefe und Kurtosis
Mit Hilfe des Histogramms kannst du besonders bei metrischen Variablen die Verteilung analysieren. Du kannst erste Eindrücke darüber sammeln, ob die Verteilung linksschief oder rechtsschief ist, ob sie Wölbungen hat und ob sie einen oder mehrere Gipfel hat.
Wie würdest du das oben gezeigte Histogramm interpretieren? Schau dir dazu noch einmal verschiedene Verteilungsformen an:
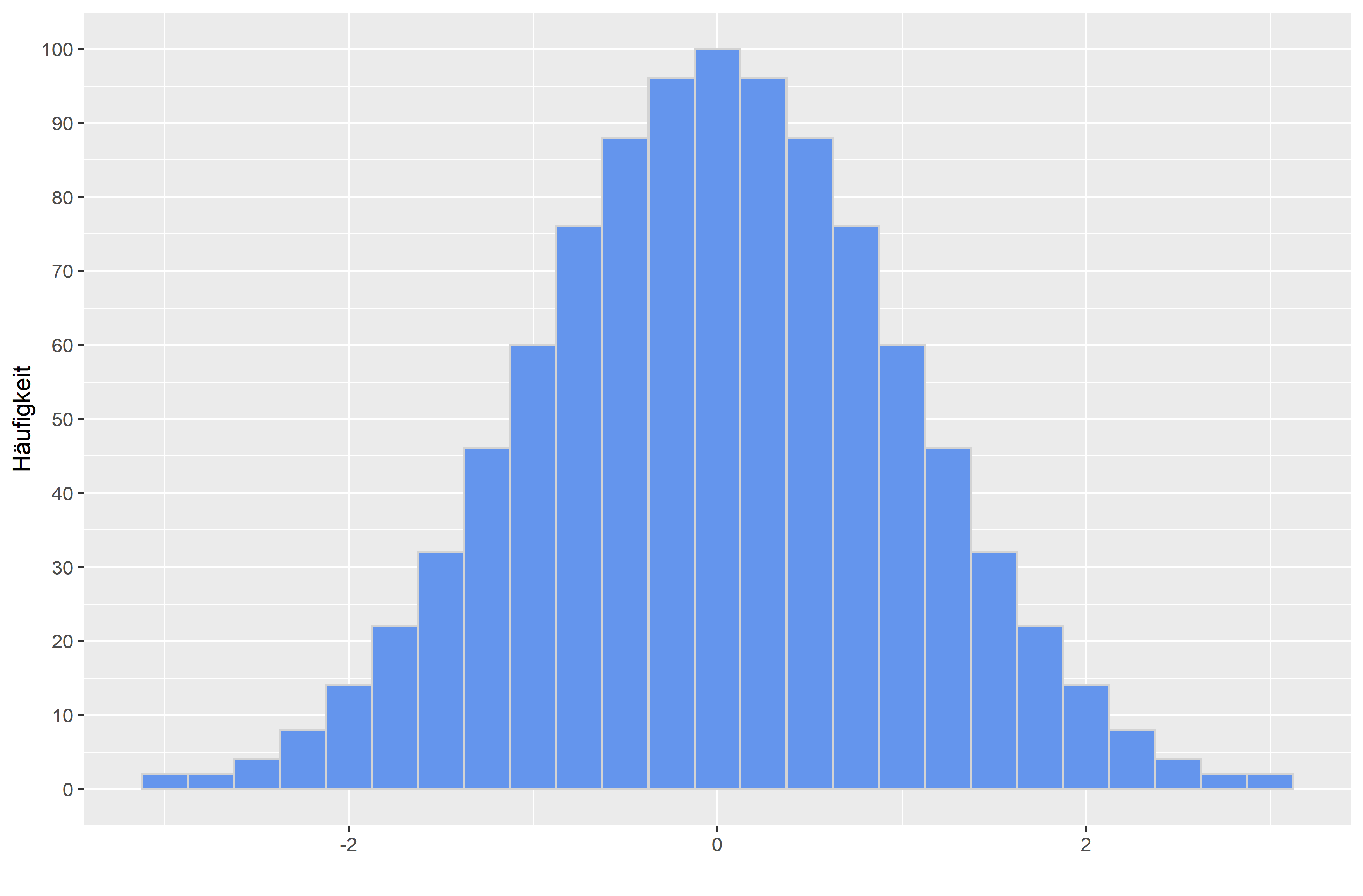
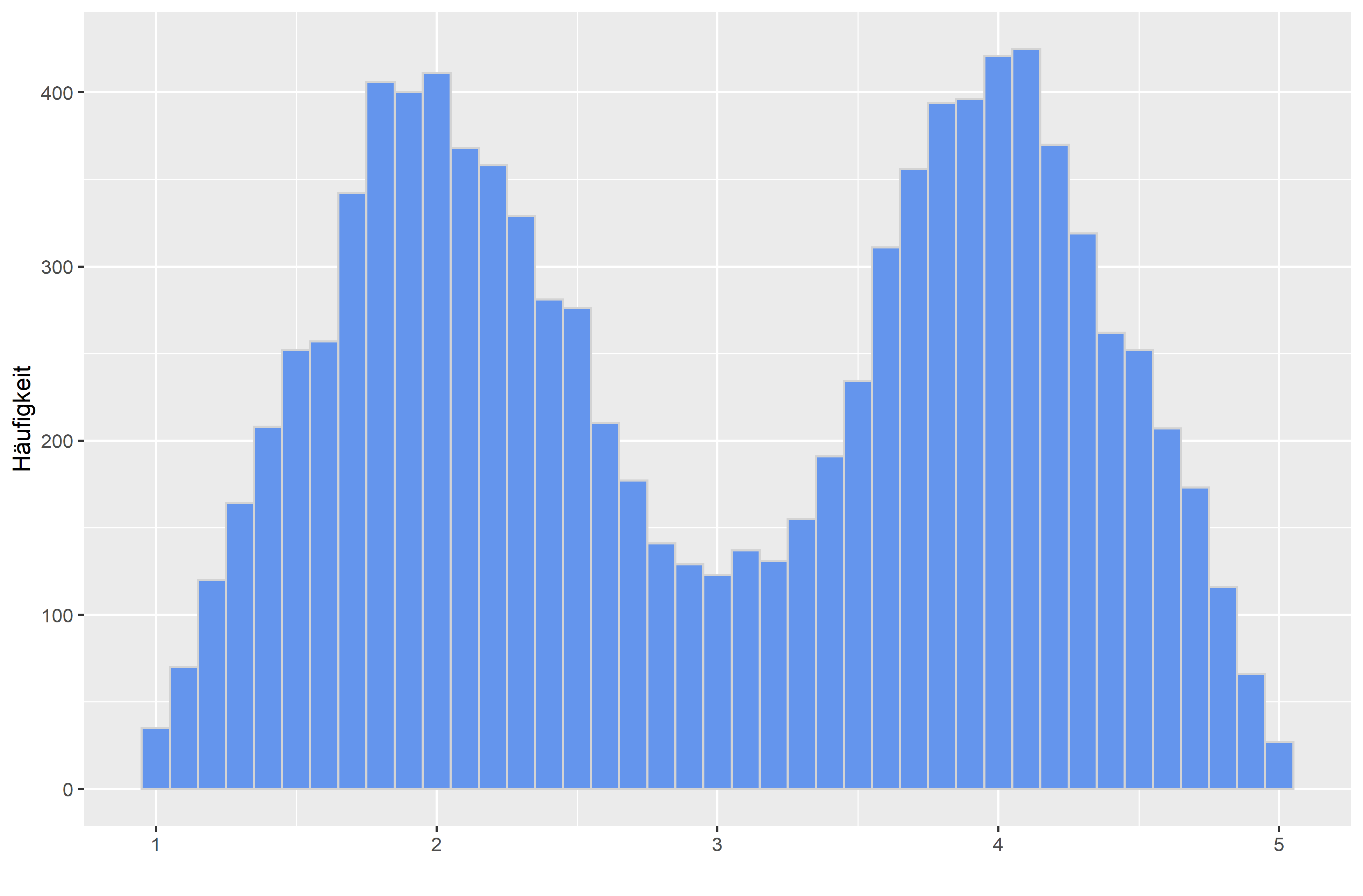
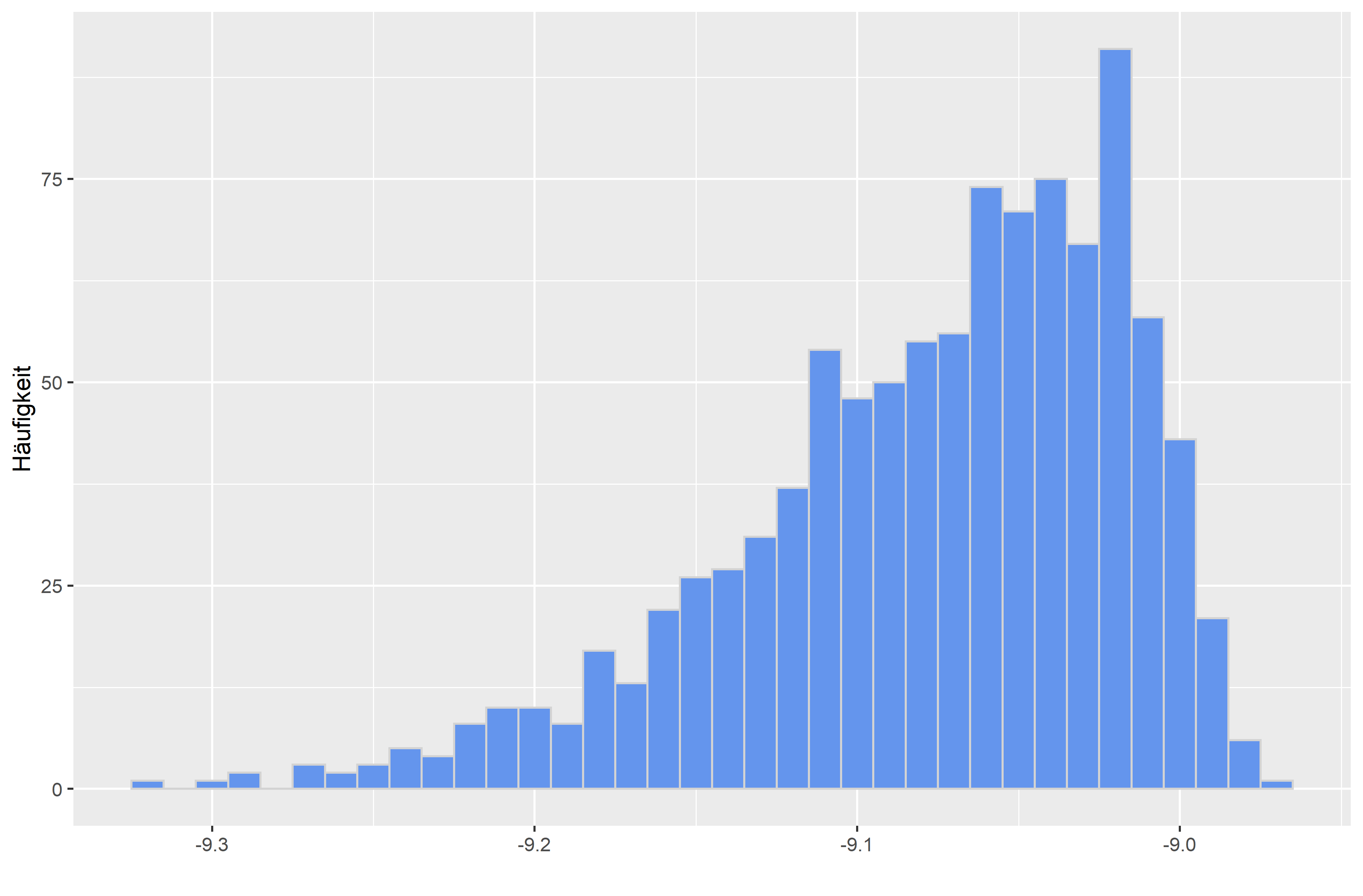
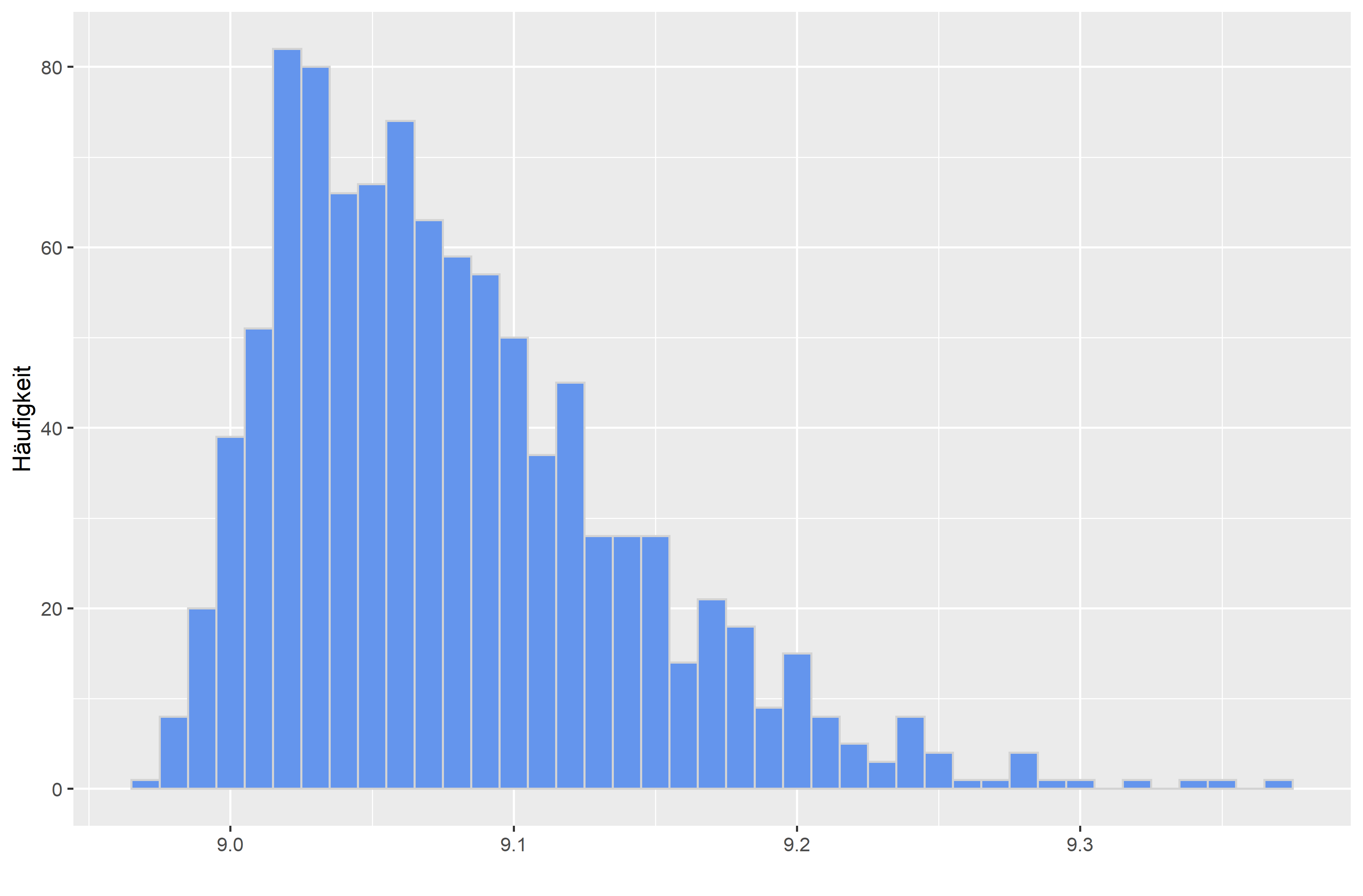
Zwei Kennwerte beschreiben quantitativ diese Dinge. Ist die Schiefe unter 0, handelt es sich um eine rechtsschiefe Verteilung. Ist sie über 0, handelt es sich um eine linksschiefe Verteilung. Ist die Kurtosis gleich 0, handelt es sich um eine eingipflige Normalverteilung. Ist sie über 0, handelt es sich um eine steilgipflige Verteilung. Ist sie unter 0, handelt es sich um eine breitgipflige Verteilung.
Du kannst dir auch mit Frequencies die Schiefe und Kurtosis ausgeben lassen. Dafür musst du nur die jeweiligen Paramter nach /STATISTICS eingeben.
FREQUENCIES VARIABLES=wkhtot
/STATISTICS=SKEWNESS KURTOSIS.
Die neuen Parameter lauten SKEWNESS und KURTOSIS. Einfach Schiefe und Kurtosis auf englisch, easy!
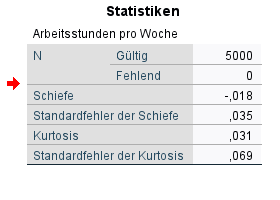
Diesen Statistik-Output kennst du bereits. Jetzt gibt er dir die Schiefe und die Kurtosis an. Wir sehen also anhand der Werte, dass die Verteilung, wie bereits oben festgestellt, nahezu perfekt eine Normalverteilung aufweist.
Exkurs II die Normalverteilung
Die Normalverteilung ist ein Verteilungsmodell für metrische Variablen. Sie unterstellt eine symmetrische Verteilungsform in Form einer Glocke, bei der sich die Werte der Variablen in der Mitte der Verteilung konzentrieren und mit größerem Abstand zur Mitte immer seltener auftreten. Die Normalverteilung gilt als das wichtigste Verteilungsmodell der Statistik und wird für unterschiedlichste Zwecke verwendet. Sie ist oft Grundlage für zentrale statistische Analyseverfahren. In der empirischen Praxis werden viele Verfahren allerdings auch angewandt, wenn keine Normalverteilung festgestellt werden kann, da viele Verfahren robust gegenüber dieser Verletzung sind. Du solltest dir aber trotzdem die Verteilungen der Variablen anschauen und dies sowohl bei der Beschreibung der Daten als auch bei der Interpretation der Ergebnisse berücksichtigen.
Boxplots
Boxplots sind sehr beliebt für die univariate Darstellung von Variablen. An ihnen kannst du Lageparameter und Informationen über die Verteilung ablesen. Besonders geeignet sind sie zum Erkennen von Ausreißern oder zum Vergleichen zwischen zwei oder mehreren Gruppen. Schauen wir uns dafür an, wie die Arbeitszeit nach Geschlecht verteilt ist.
EXAMINE VARIABLES=wkhtot BY gndr
/PLOT=BOXPLOT
/STATISTICS=NONE
/NOTOTAL.
Die Boxplots werden mit einem neuen Hauptbefehl EXAMINE gebildet. Vor dem Parameter BY definierst du die Variable, die im Boxplot dargestellt werden soll. Nach dem Parameter BY definierst du die Variable, nach der gruppiert werden soll. Im Argument /PLOT=BOXPLOT geben wir an, dass ein Boxplot ausgegeben werden soll. Danach geben wir, dass wir keine Ausgabe von statistischen Kennzahlen benötigen (/STATISTICS=NONE). Zuletzt sagen wir, dass wir nur die getrennten Boxplots ausgeben lassen wollen, und kein drittes über alle Werte (/NOTOTAL).
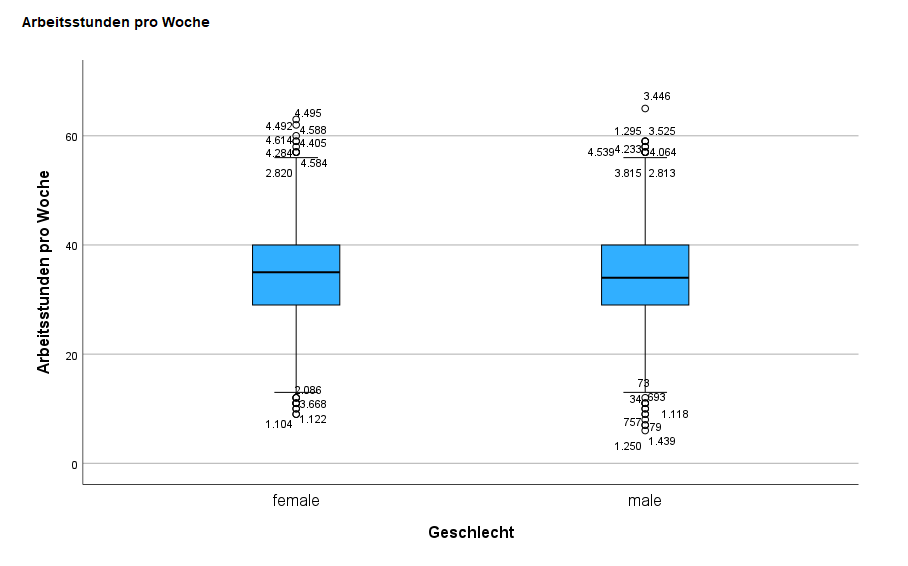
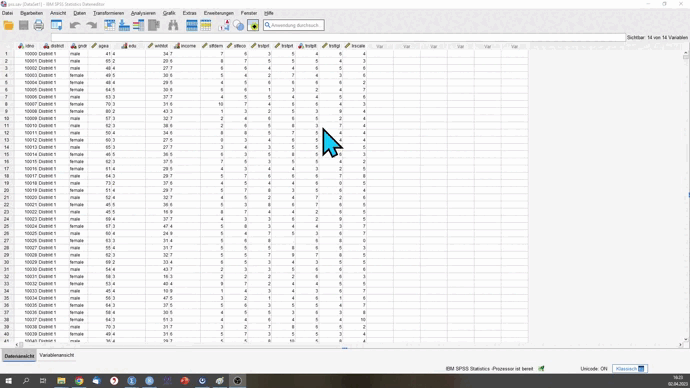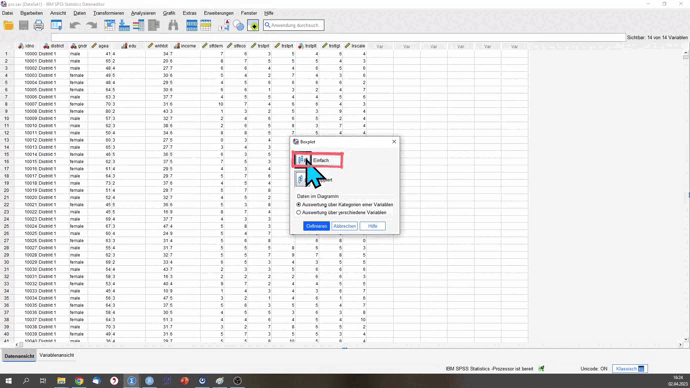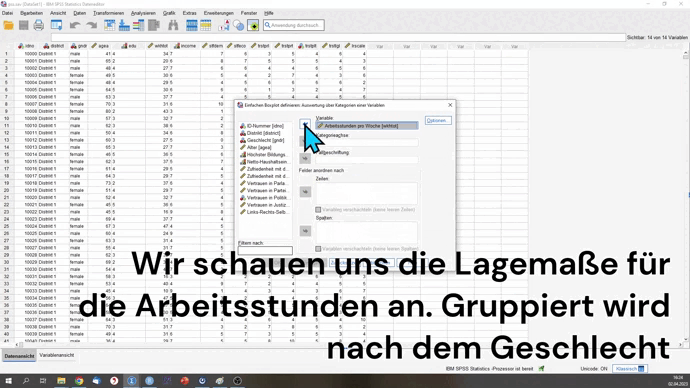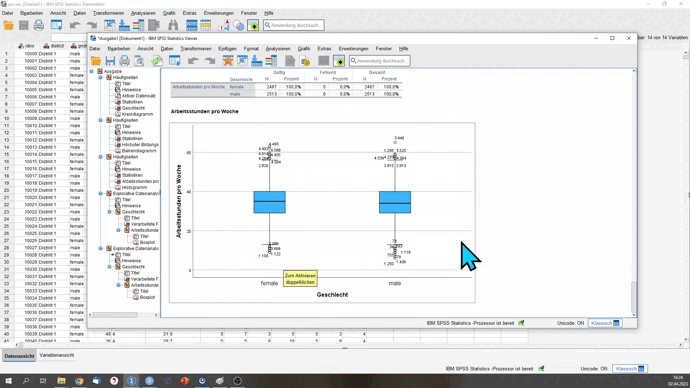
Am oberen und unteren Ende der Box siehst du relevante Ausreißer. Als Ausreißer definiert SPSS alle Fälle, die mehr als das anderthalbfache der Boxhöhe (dem Interquartilsabstand) von der Box entfernt sind. Diese sind mit einem Punkt dargestellt. Die dazugehörigen Nummern geben die Zeile des Falls in der Datenansicht wieder. Die blaue Box selbst umschließt das erste und das dritte Quartil (Abstand zwischen diesen ist der Interquartilsabstand). Der Strich in der Box symbolisiert den Median. Die beiden Striche außerhalb der Box symbolisieren den größten und den kleinsten Wert auserhalb der Box, der nicht als Ausreißer gilt.
Hier sehen wir also, dass es scheinbar zwischen den Geschlechtern kaum Unterschiede in der wöchentlichen Arbeitszeit gibt.
So, nun hast du den Lernblock erfolgreich beendet!