Grundgesamtheit & Stichprobe
Um auf der Mikroebene sozialwissenschaftliche Untersuchungen durchführen zu können, die generalisierbar sind, werden Stichproben aus der Grundgesamtheit gezogen. Dies ist notwendig, da in den seltensten Fällen Vollerhebungen durchgeführt werden können. Sie können z.B. nur sehr schwer und unter hohen Kosten eine Vollerhebung der Bürger*innen Deutschlands durchführen, eine Stichprobe aus dieser Grundgesamtheit lässt sich aber kostengünstiger und einfacher umsetzen.
Bei der Ziehung von Stichproben unterscheiden wir drei Begriffe: Grundgesamtheit (auch Zielpopulation), Auswahlgesamtheit und Survey-Population (auch Inferenzpopulation). Diese Unterscheidung ist wichtig, um das Ziehen einer Stichprobe möglichst genau zu verstehen. Bei der Ziehung von Stichproben kommt es nämlich zu Ausfällen. Die Zielpopulation (auch angestrebte Grundgesamtheit) ist die Menge aller Einheiten, über die wir eine Aussage treffen wollen.
Nehmen wir das Beispiel an, dass wir eine Wahlstudie in Deutschland durchführen möchten. Die Zielpopulation wären dann alle wahlberechtigten Personen zum Zeitpunkt der Erhebung.

Die Auswahlgesamtheit stellt die Personen dar, die auch tatsächlich in die Auswahl der Stichprobe kommen können. Personen in der Auswahlgesamtheit haben also eine Wahrscheinlichkeit von größer als \(0\), Teil der Stichprobe zu sein. Die Auswahlgesamtheit unterscheidet sich von der Zielpopulation aufgrund des Auswahlmechanismus.
Nehmen wir wieder unser Beispiel: Unsere Wahlstudie möchten wir mit einer Stichprobe durchführen, die wir über Festnetztelefone machen. Damit umfasst die Auswahlgesamtheit alle Personen, die einen Festnetzanschluss in Deutschland haben. Personen, die wahlberechtigt sind und keinen Festnetzanschluss haben, können somit nicht Teil unserer Auswahl werden. Diese Personen haben eine Wahrscheinlichkeit von \(0\), Teil der Stichprobe zu sein. Diesen Ausschluss von Personen, die eigentlich zur Grundgesamtheit gehören, aber nicht Teil der Auswahlgesamtheit sind, bezeichnet man auch als undercoverage.
Gegensätzlich könnten wir Personen über einen Festnetzanschluss erfassen, die zum Beispiel gar nicht wahlberechtigt sind. Dies trifft zum Beispiel auf viele EU-Bürger.innen zu, die in Deutschland leben, aber nur an kommunalen Wahlen und nicht an Bundestags- und Landtagswahlen teilnehmen dürfen. Diese Personengruppe wird als overcoverage beschrieben. Denn sie ist nicht Teil der Zielpopulation, kann aber in der Auswahlgesamtheit gefasst sein. Die Gruppe der Personen aus dem overcoverage sind in aller Regel aber identifizierbar und können ausgeschlossen werden.
Für die Survey-Population ergibt sich dann aus dem „gemeinsamen“ Bereich von Zielpopulation und Auswahlgesamtheit, overcoverage und undercoverage die tatsächliche Stichprobe.
Neben diesen Differenzen aus overcoverage und undercoverage kann es dazu kommen, dass Personen, die aus der Auswahlgesamtheit gezogen wurden, dennoch nicht in der Survey-Population berücksichtigt werden. Dies liegt oftmals an der Verweigerung der gezogenen Person, dem Ausfall der Person oder auch an Fehlern in der Datenverarbeitung, so dass einzelne Daten verloren gehen.
Warum Zufallsstichproben gezogen werden, um Rückschlüsse auf die Grundgesamtheit zu ziehen, ist mithilfe des Grenzwertsatzes der großen Zahlen zu erklären. Wenn wir unendlich viele Stichprobe ziehen, wird sich der Mittelwert dieser Stichproben, dem Grenzwertsatz der großen Zahlen nach, immer an den wahren Mittelwert der Grundgesamtheit annähern. Der Grenzwertsatz der großen Zahlen wird ausführlicher im Kapitel Mathematische Grundlagen behandelt.
Aus dieser Logik heraus erfolgt die Zufallsauswahl bei Befragungen in den Sozialwissenschaften: Wir definieren eine Grundgesamtheit, aus der eine Stichprobe per Zufall gezogen wird. Mit welchen Fehlern diese Zufallsstichprobe gezogen wird, können wir festhalten und diese Fehler berücksichtigen, bevor Rückschlüsse auf die Verteilung in der Grundgesamtheit geschlossen werden. In den analytischen Verfahren werden anhand der Stichprobenstatistik Aussagen getroffen, die dann in der aggregierten Form (Kennwerte einer Stichprobe) per Inferenz auf den wahren Durchschnitt der Grundgesamtheit übertragen werden. Mathematisch wird der wahre Wert (Erwartungswert) einer Grundgesamtheit mit dem griechischen Buchstaben \(\mu\) (mü) bezeichnet. Die folgenden Abbildungen verdeutlicht das Verfahren noch einmal.
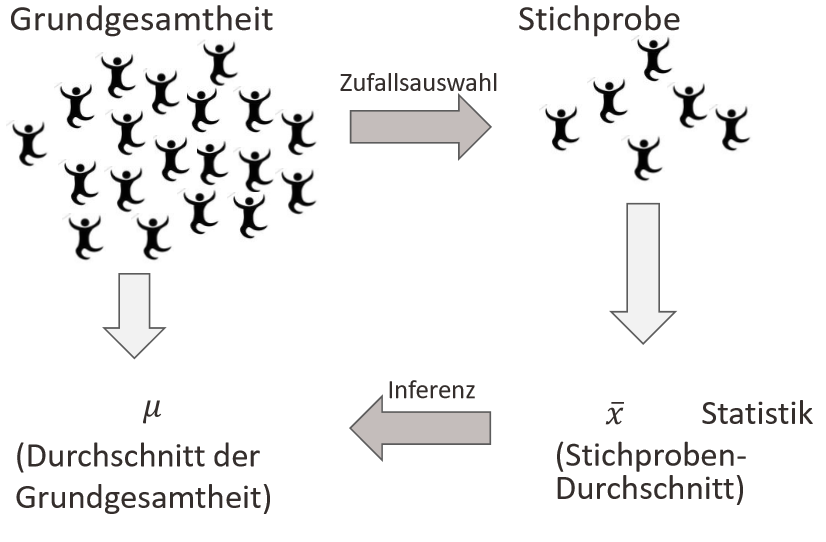
Um Stichproben zu ziehen, gibt es zufallsbasierte und nicht-zufallsbasierte Stichprobenziehungen. Nur mit zufallsbasierten Stichprobenziehungen ist ein Rückschluss mithilfe der Inferenzstatistik möglich. Nun werden Ihnen zur Abgrenzung nicht-zufallsbasierte Verfahren (bewusste Auswahl, willkürliche Auswahl, Quota-Verfahren) vorgestell und darauf aufbauend die zufallsbasierten Stichprobenziehungen (einfache Zufallsauswahl, Schichtung, Klumpenstichprobe).