Kreuztabellen mit relativen Häufigkeiten
Eine Kreuztabelle gibt Auskunft über eine bivariate Verteilung, also über die Verteilung auf zwei Variablen. Wenn wir relative Häufigkeiten untersuchen wollen, müssen wir zuerst das Relativ bestimmen, auf das sich die Prozentwerte beziehen. Wir definieren sozusagen die 100%, auf die sich die einzelne Zelle beziehen soll. Es gibt hierbei drei zentrale möglichkeiten:
-
Prozentwerte bezogen auf die Zeilenvariable
-
Prozentwerte bezogen auf die Spaltenvariable
-
Prozentwerte bezogen auf die gesamte Fallzahl der Kreuztabelle.
Bevor wir uns die zeilen- und spaltenweise Prozentuierung anschauen, schauen wir uns noch kurz Randhäufigkeiten an. Als Randhäufigkeiten bezeichnet man den rechten und unteren Rand einer Kreuztabelle. Diese Informationen sind deskriptiver Natur und hätten wir auch durch eine univariate Häufigkeiten herausbekommen können.

Prozentuierung bezogen auf die Zeilen
Wenn wir Prozentwerte bezogen auf die Zeilen untersuchen wollen, definieren wir die Randhäufigkeiten am rechten Rand als unser Relativ. Sie erhalten den Prozentwert von 100%. Ausgehend von diesen 100% können wir nun innerhalb einer Zeile die relativen Häufigkeiten bezogen auf den jeweiligen 100%-Wert derselben Zeile analysieren. Schau dir das Beispiel dafür an.
CROSSTABS
/TABLES=edu BY gndr
/CELLS=COUNT ROW.
Im Unterbefehl /CELLS können wir mit Hilfe der Parameter die Prozentuierung festlegen. ROW ist der Parameter für die Prozentuierung bezogen auf die Zeilen
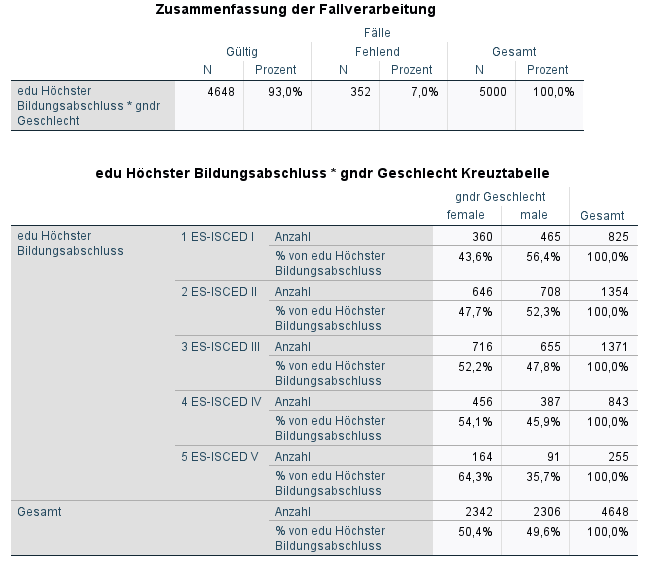
Wie du siehst, wurde die komplette rechte Spalte als Relativ definiert. Bei der Interpretation bist du immer auf der sicheren Seite, wenn du von dem Relativ ausgehst. Also: Von allen Befragten mit einem Schulabschluss erster Stufe (Relativ) sind 43.6% weiblich und 56.4% männlich. Weiteres Beispiel: Von allen Befragten mit einem Schulabschluss fünfter Stufe sind 64.3% weiblich und 35.7% männlich. Die Interpretation von Prozentwerten in einer Kreuztabelle ist sehr fehleranfällig. Wenn du aber dieser Faustregel folgst, machst du es immer richtig!
Prozentuierung bezogen auf die Spalten
Diese Art der Prozentuierung ist die Konvention in den Sozialwissenschaften. Wichtig ist dazu zu wissen, dass wir so eine Abhängigkeit mit der Prozentuierung erstellen: Die Spaltenvariable wirkt auf die Zeilenvariable. In die Spalte kommt also die unabhängige Variable und in die Zeile die abhängige Variable. In diesem Fall würden wir also davon ausgehen, dass der formale Bildungsgrad vom Geschlecht abhängt.
Wenn wir Prozentwerte bezogen auf die Spalten untersuchen wollen, definieren wir die Randhäufigkeiten am unteren Rand als unser Relativ. Diese erhalten also den Prozentwert von 100%. Ausgehend von diesen 100% können wir nun innerhalb einer Spalte die relativen Häufigkeiten bezogen auf den jeweiligen 100%-Wert derselben Spalte analysieren. In diesem Beispiel werden dieselben Variablen verwendet. Merkst du den Unterschied zwischen dieser und der ersten Prozentierung? Also, immer die Prozentuierung bei einer Kreuztabelle beachten!
CROSSTABS
/TABLES=edu BY gndr
/CELLS=COUNT COLUMN.
Im Unterbefehl /CELLS können wir mit Hilfe der Parameter die Prozentuierung festlegen. COLUMN ist der Parameter für die Prozentuierung bezogen auf die Spalten
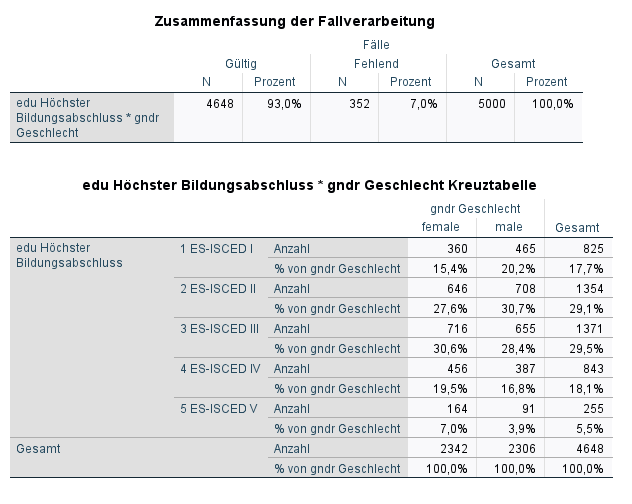
Wie du siehst, wurde die komplette untere Zeile als Relativ definiert. Zur Erinnerung: Bei der Interpretation bist du immer auf der sicheren Seite, wenn du von dem Relativ ausgehst. Also: Von allen Befragten, die weiblich sind, haben 15.4% einen Schulabschluss erster Stufe, 27.6% einen Schulabschluss zweiter Stufe, und so weiter und so fort. Weiteres Beispiel: Von allen Befragten, die männlich sind, haben 20.2% einen Schulabschluss erster Stufe, 30.7% einen Schulabschluss zweiter Stufe, und so weiter und so fort.
Prozentuierung bezogen auf die gesamte Fallzahl
Oh je, jetzt sind ja keine Randhäufigkeiten mehr übrig, um sie als Relativ zu bestimmen. Dann bestimmen wir jetzt die gesamte Fallzahl als Relativ. Diese findest du in einer Kreuztabelle immer ganz unten rechts. Du liest jetzt den Prozentwert jeder Zelle immer in Abhängigkeit zum Gesamtwert. Du kannst die Werte auch wie eine Typologie interpretieren. Das Beispiel verwendet wieder dieselben Variablen. Unten siehst du, wie wir das interpretieren.
CROSSTABS
/TABLES=edu BY gndr
/CELLS=COUNT TOTAL.
Im Unterbefehl /CELLS können wir mit Hilfe der Parameter die Prozentuierung festlegen. TOTAL ist der Parameter für die Prozentuierung bezogen auf die Spalten
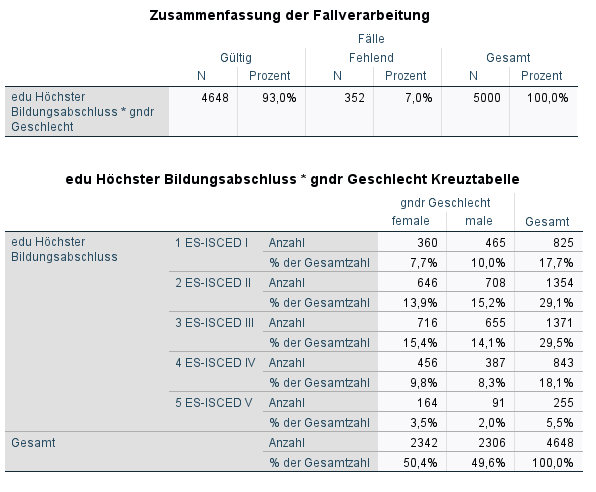
Jetzt ist die gesamte Fallzahl als Relativ definiert. Das ist immer das Feld ganz unten rechts. Auch hier bist du bei der Interpretation immer auf der sicheren Seite, wenn du von dem Relativ ausgehst. Also: Von allen Befragten (das ist hier das Relativ) sind 7.7% weiblich und haben einen Schulabschluss erster Stufe. Weiteres Beispiel: Von allen Befragten sind 10% männlich und haben einen Schulabschluss erster Stufe.
Faustregeln zur Interpetation
Zwar bietet die Kreuztabellen viele verschiedene möglichkeiten zur Anlage an. Aber keine Sorge. Es gibt auch ein paar Konventionen, die dir eine Orientierung geben können. Als Basis der Prozentuierung nehmen wir nämlich meistens Spaltenprozentwerte, also mit /CELLS = COUNT COLUMN. Dafür packen wir unsere unabhängige Variable in die Spalten. Grundsätzlich ist aber auch das Ausprobieren durchaus in Ordnung. Gerade, wenn du nicht weißt, welche Variable die unabhängige und welche die abhängige ist. Wichtig ist dabei, dass du trotzdem die Prozentwerte korrekt, wie oben dargstellt, interpretierst. Das ist erfahrungsgemäß eine häufige Fehlerquelle.
Wie können wir jetzt Unterschiede bei den Prozentwerten interpretiern? Ab welchem Unterschied können wir von einem starken oder geringen Unterschied sprechen. Kühnel und Krebs (2006) haben dafür Faustregeln aufgestellt.
-
Differenzen unter 5 Prozentpunkten gelten als nicht interpretierbar.
-
Differenzen unter 10 Prozentpunkten gelten als gering.
-
Differenzen unter 25 und mehr Prozentpunkten weisen auf einen starken Zusammenhang hin.
Beachte aber: Abweichungen von der Faustregeln sind vor dem Hintergrund der Verteilung und der Fallzahl deines Datensatzes durchausmöglich. Überschätze also diese Faustregeln nicht. Beachte auch, dass eine Zelle idealerweise mindestens 15 Fälle beinhalten sollte. Jedoch kommt es selbst bei großen Datensätzen in der Praxis besonders bei Variablen mit vielen Ausprägungen oft vor, dass Zellen gering besetzt sind oder sogar leer sind. Letzteres ist das sogenannte Nullzellenproblem und oft für die Berechnung statistischer Maßzahlen ein ernstzunehmendes Problem.
Apropos statistische Maßzahlen, machen wir damit mal gleich weiter.