Korrelationen
Machen wir weiter mit Pearson’s R. Eine Korrelation nach Pearson’s R beschreibt in erster Linie einen linearen Zusammenhang zwischen zwei Variablen. Aber nicht vergessen: Eine Korrelation trifft keine Aussage zur Kausalität. Ein Korrelationskoeffizient misst nur, ob sich zwei Merkmale im linearen Gleichklang bewegen.
Für die Berechnung von Pearson’s r müssen folgende Bedingungen erfüllt sein:
(pseudo-)metrische Variablen
lineare (monotone) Beziehung
Varianzgleichheit
(bivariate Normalverteilung)
SPSS gibt uns bei der Analyse von Korrelationen auch Spearman’s \(\rho\) aus. Diese Maßzahl wird bei ordinal-skalierten Variablen genutzt oder wenn die Beziehung nicht linear ist. Für die Berechnung von Spearman’s \(\rho\) müssen dagegen nur folgende Bedingungen erfüllt sein:
(mind.) ordinale Variablen
monotone Beziehung
Lineare und nicht lineare Beziehungen
In der Abbildung sind vier Beispiele vorgestellt, die alle nahezu gleiche statistische Maßzahlen erreichen (Ascombe-Quartett).
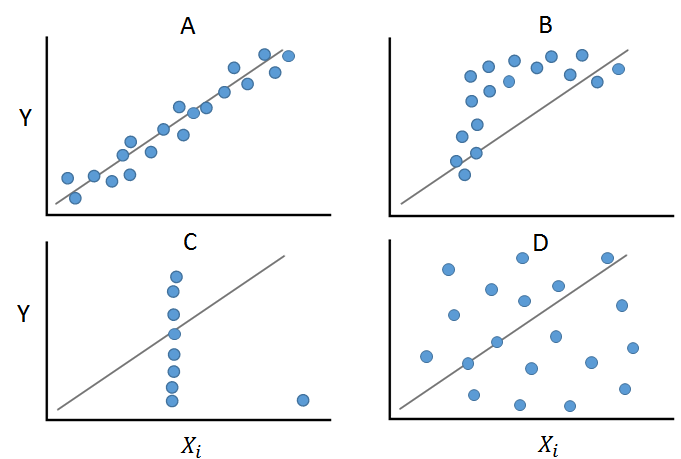
Feld A zeigt eine lineare und monotone Beziehung zwischen zwei Variablen. Hier wäre die Anwendung der Berechnung von Pearson’s r korrekt. Feld B zeigt zwar eine monotone Beziehung, diese ist aber nicht linear. In diesem Fall kann Spearman’s \(\rho\) berechnet werden. Feld C zeigt, wie ein Ausreißer die Beziehungsstruktur verändern kann und hier würden beide Korrelationsmaße einen verzerrten Wert ausgeben. Feld D zeigt eine nicht lineare wie nicht-monotone Beziehung.
Deutlich wird hier, dass vor der Berechnung von Maßzahlen die grafische Analyse hilfreich bzw. erforderlich ist!
Interpretation von Pearson’s R
Fassen wir Pearson’s R zusammen.
Es untersucht einen Zusammenhang auf Stärke, Signifikanz, Richtung und Linerität. Ein Wert von \(r = 1\) ist ein perfekter, positiver, linearer Zusammenhang, ein Wert von \(r = 0\) bedeutet kein Zusammenhang und ein Wert von \(r = -1\) ist ein perfekter, negativer, linearer Zusammenhang.
Dabei hat SPSS mehrere Voraussetzungen. Die Annahme eines lineares Zusammenhanges können wir mit SPSS grafisch prüfen (siehe unten).
Pearson’s R misst die Schlankheit der Punktewolke. Je mehr die Punkte eine lineare Linie ergeben, desto größer ist Pearson’s R.
Auch für Pearson’s R gibt es Faustregeln zur Interpretation der Stärke eines Zusammenhanges
Diese Werte gelten für den positiven und negativen Bereich
| unteres Ende | oberes Ende | Interpretation |
|---|---|---|
| \(0\) | \(0.05\) | zu vernachlässigen |
| \(0.05\) | \(0.2\) | geringer linearer Zusammenhang |
| \(0.2\) | \(0.5\) | mittlerer linearer Zusammenhang |
| \(0.5\) | \(0.7\) | stark linearer Zusammenhang |
| \(0.7\) | \(1\) | sehr starker linearer Zusammenhang |
Grafisch auf Linearität prüfen.
Nun sollst du die Korrelation zwischen Trust in Parliament (trstprl) und Trust in Politicians (trstplt) aus dem PSS berechnen.
Beide Variablen sind pseudo-metrische Variablen, daher solltest du Pearson’s r berechnen.
Dafür testen wir grafisch, ob die Annahme der Linearität gegeben ist. Dafür gibt es eine einfache Syntax, die besser zu bedienen ist, als der komplexe Diagrammeditor in SPSS.
IGRAPH
/Y=trstprl TYPE=SCALE
/X1=trstplt TYPE=SCALE
/SCATTER COINCIDENT=JITTER.
Der Hauptbefehl lautet IGRAPH. Unter /Y und /X1 definierst du die y-Achse und die x-Achse. Mit dem Parameter JITTER erhältst du eine angenehm interpretierbare Grafik.
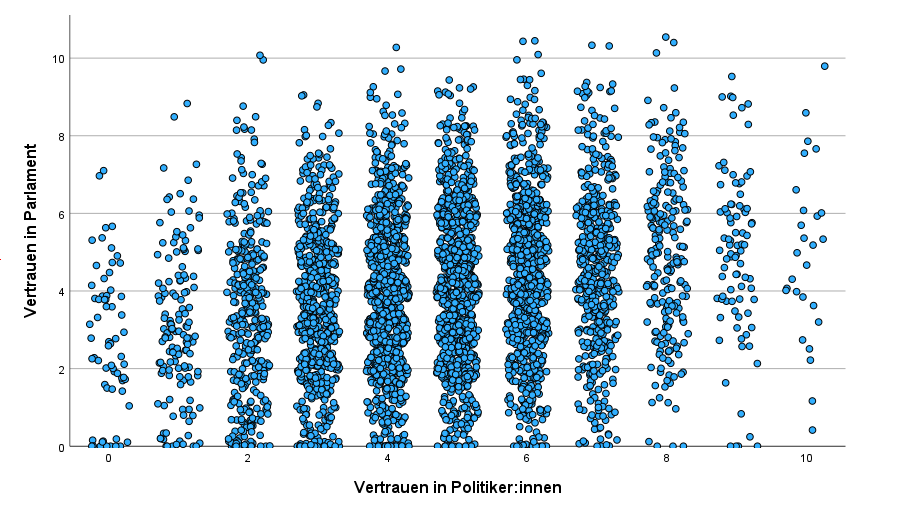Mit dieser Grafik kannst du erahnen, dass es sich um einen linearen Zusammenhang handeln könnte. Der Parameter JITTER sorgt für ein zufälliges Hintergrundrauschen. Daher sind die Punkte nicht wie Perlen an einer Kette entlang einer Ausprägung orientiert, sondern schwanken ein wenig um sie herum, sodass die Grafik besser zu interpretieren ist.
Abschließend können wir also festhalten, dass die Bedingungen erfüllt sind:
Stichprobe von verbundenen Werten \(\checkmark\)
beide Variablen metrisch \(\checkmark\)
Beziehung zwischen Variablen ist linear \(\checkmark\)
\(\Rightarrow\) Du kannst nun Pearson’s R berechnen!
Interpretation Spearman’s \(\rho\)
Zur Wiederholung: Den Rangkorrelationskoeffizient nach Spearman verwenden wir, um den Zusammenhang zwischen zwei mindestens ordinalskalierten Variablen zu bestimmen. Anders als bei Pearson’s R muss hier die Annahme der Linearität nicht geprüft werden. Auch bei Spearman’s \(\rho\) können wir die Stärke und Richtung des Zusammenhanges benennen. Die Werte reichen von \(-1\) bis \(+1\). Du kannst den Wert mit derselben Faustregel wie oben interpretieren.
Berechnen der Koeffizienten
Um den Korrelationskoeffizienten zu berechnen, können wir mit dem Befehl CORRELATIONS oder mit den Kreuztabellen CROSSTABS arbeiten. Schauen wir uns zunächst letzteres an.
CROSSTABS
/TABLES=trstplt BY trstprl
/STATISTICS=CORR
/CELLS=COUNT.
Den Hauptbefehl kennst du bereits. Wie bei Cramer’s V oder Gamma können wir hier mit einem Parameter das gewünschte Zusammenhangsmaß ausgeben lassen. Dieser lautet sowohl für Pearson’s r als auch Spearman’s \(/rho\) CORR.
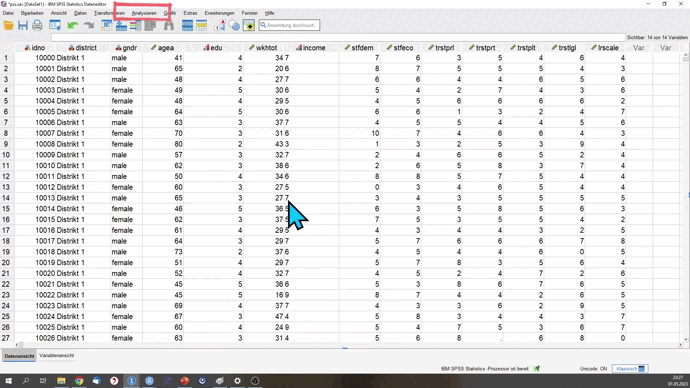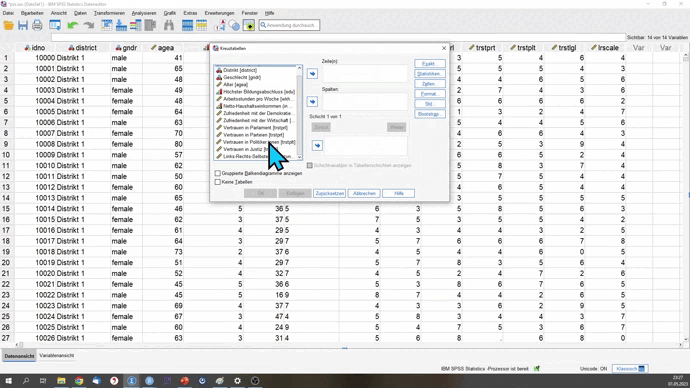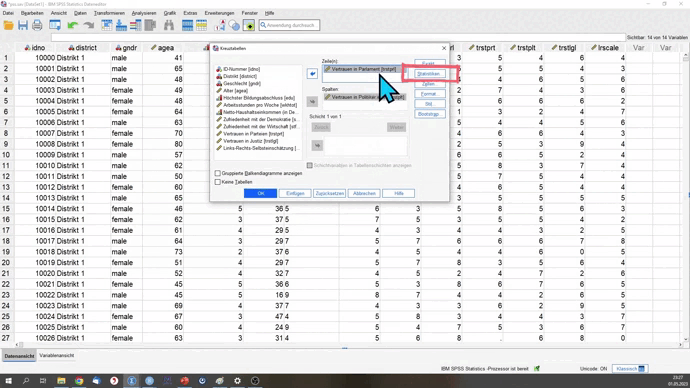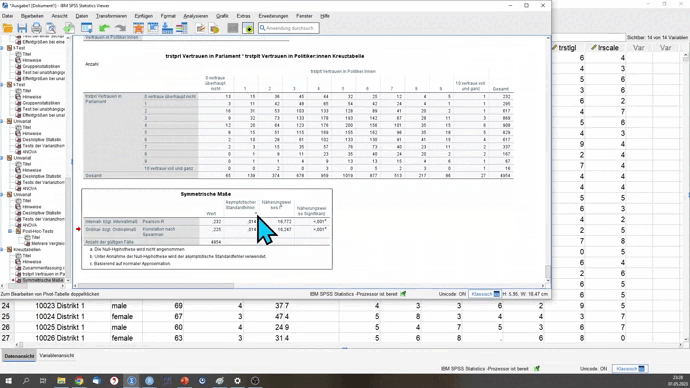
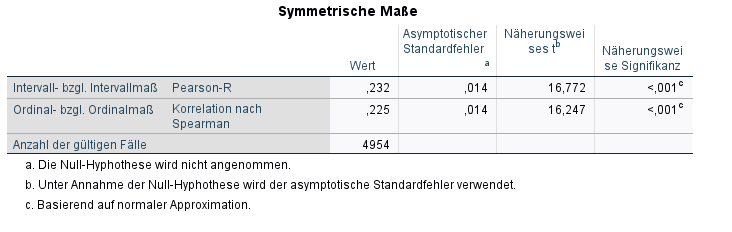Wie du siehst, liefern beide Maßzahlen unterschiedliche Werte. Daher ist es besonders wichtig, die richtige Maßzahl für das Skalenniveau auszuwählen.
Die Korrelationsmatrix
Mit dem Befehl CORRELATIONS, beziehungsweise NONPAR CORR kannst du nicht nur die Korrelation zwischen zwei Variablen berechnen, sondern direkt mehr als zwei Variablen angeben. Es wird dann jeweils paarweise zwischen allen Variablen die Korrelation berechnet.
Hierbei ist es wichtig, dass du dir Gedanken über den Fallausschluss machst.
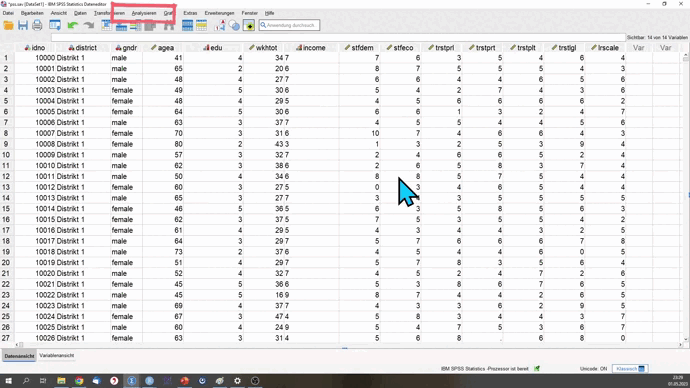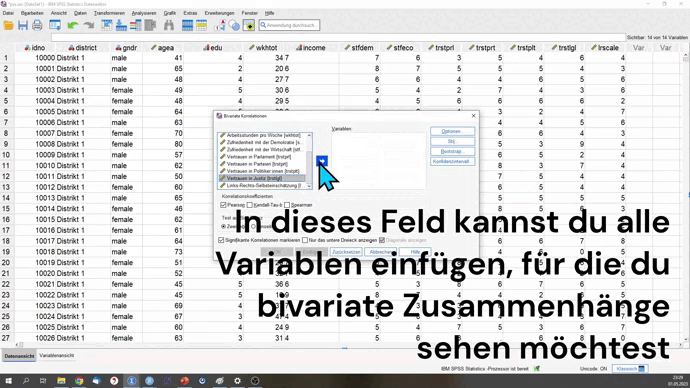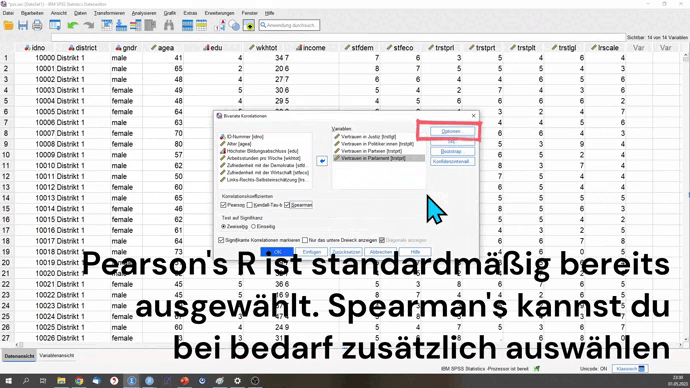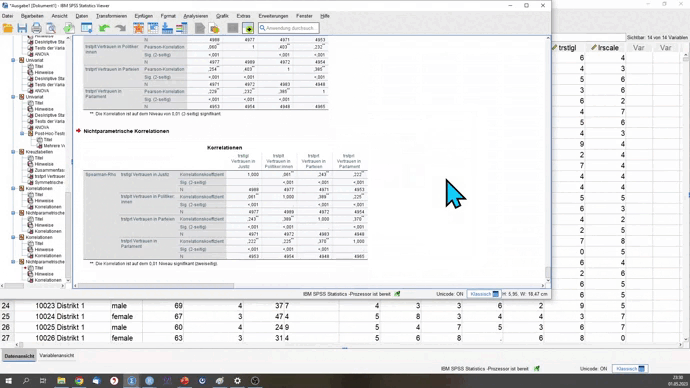
CORRELATIONS
/VARIABLES=trstprl trstprt trstplt trstlgl
/PRINT=TWOTAIL NOSIG FULL
/MISSING=PAIRWISE oder LISTWISE.
NONPAR CORR
/VARIABLES=trstprl trstprt trstplt trstlgl
/PRINT=SPEARMAN TWOTAIL NOSIG FULL
/MISSING=PAIRWISE oder LISTWISE.
Für Pearson’s R gibt es den Hauptbefehl CORRELATIONS. Nach /VARIABLES gibst du die Variablen an, die du analysieren willst. Nach /MISSING kannst du den Fallausschluss festlegen. PARIWISE steht für den paarweisen Fallausschluss. LISTWISE steht für den listenweisen Fallausschluss.
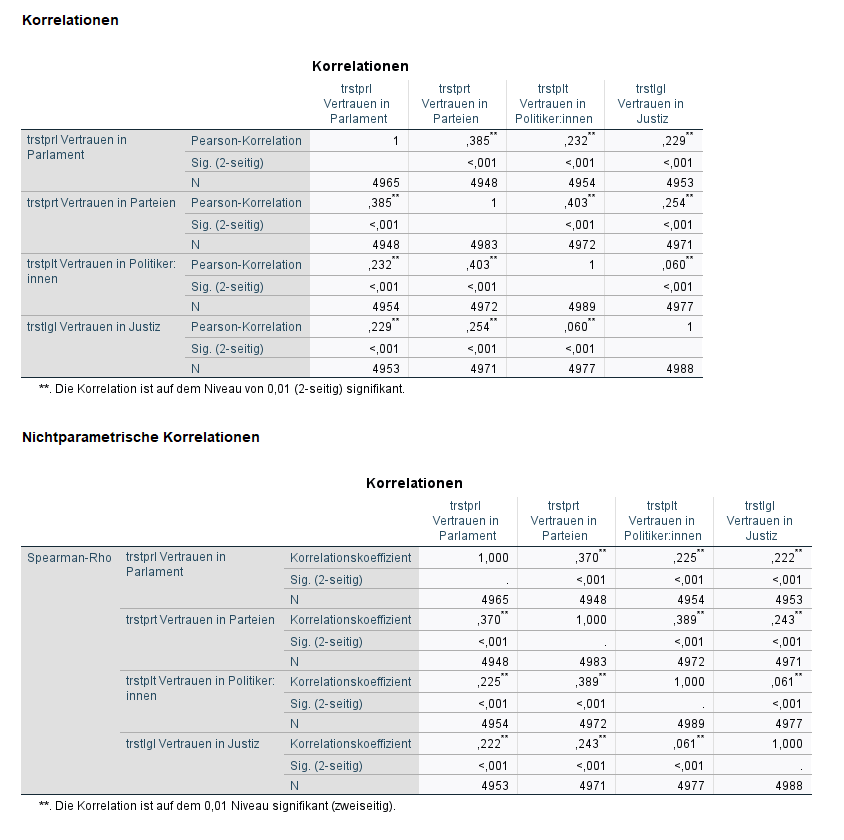
Wie du siehst liefern beide Maßzahlen unterschiedliche Werte. Daher ist es besonders wichtig, die richtige Maßzahl für das Skalenniveau auszuwählen.
Super, du kannst jetzt Zusammenhänge mit SPSS berechnen. Machen wir nun weiter mit der Analyse von Unterschieden: Dem Mittelwertvergleich.