Zwischen mehr als zwei Gruppen
Auf dieser Seite werden Mittelwertvergleiche zwischen mehr als zwei Gruppen vorgestellt. Diese Test-Statistik wird (einfaktorielle) ANOVA oder F-Test genannt. Wir möchten nun die verschiedenen Gruppen der edu-Variable testen.
Hypothesen des F-Tests
\(H_0\): Alle Gruppenmittelwerte sind in der Grundgesamtheit identisch.
\(H_1\): Mindestens zwei Gruppenmittelwerte der Grundgesamtheit unterscheiden sich.
Annahmen:
abhängige Variable ist metrisch\(\checkmark\)
unabhängige Variable ist kategorial \(\checkmark\)
Gruppen sind unabhängig voneinander \(\checkmark\)
[Normalverteilung der metr. Variable in jeder Gruppe (nötig nur für \(n \leq 25\))] \(\checkmark\)
Varianzgleichheit zwischen Gruppen
Prüfen der Annahmen
Wir möchten testen, inwieweit die Arbeitsstunden zwischen verschiedenen Bildungsgruppen differieren. Dazu nimmst du die edu-Variable, die mehrere Bildungsgruppen beinhaltet. Zuerst brauchen wir einen Output, der den Levene-Test beinhaltet.
ONEWAY wkhtot BY edu
/STATISTICS DESCRIPTIVES HOMOGENEITY.ONEWAY ist der Hauptbefehl für die ANOVA. Danach definierst du immer zuerst deine Testvariable und anschließend nach dem BY die Gruppierungsvariable. Mit dem Unterbefehl /STATISTICS lassen wir uns durch DESCRIPTIVES HOMOGENEITY den Levene-Test der Varianzgleichheit ausgeben.

Für die Überprüfung der Varianzgleichheit schauen wir uns zunächst nur die Tests der Varianzhomogenität an.
Berechnen des Tests (gleiche Varianzen)
Um den Test zu berechnen, verwenden wir hier die PostHoc-Analyse mit Bonferroni (Varianzgleichheit) durch.
ONEWAY wkhtot BY edu
/STATISTICS DESCRIPTIVES HOMOGENEITY
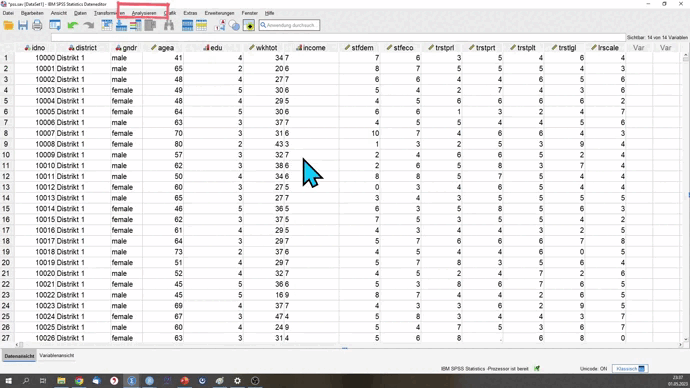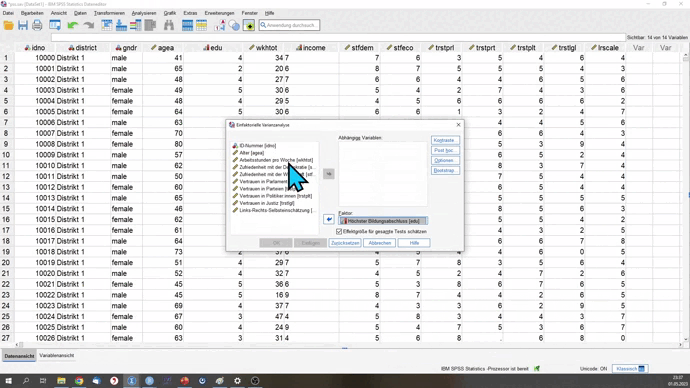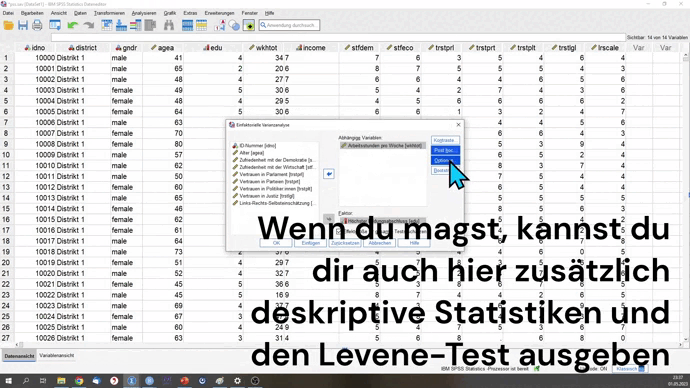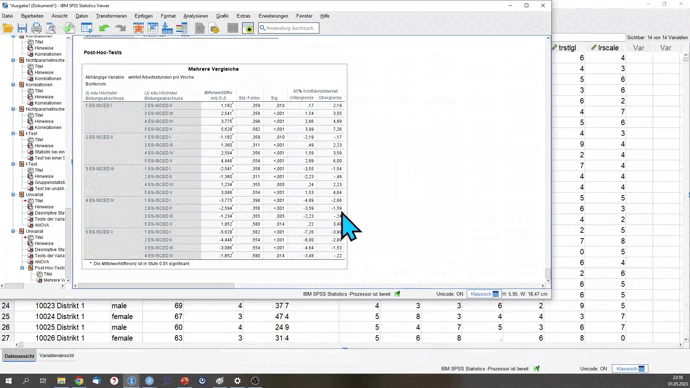
/POSTHOC=BONFERRONI ALPHA(0.05).Zusätzlich gibt es hier jetzt den Unterbefehl /POSTHOC. Wir wählen BONFERRONI, da wir Varianzgleichheit annehmen. Mit ALHPA definieren wir das Signfikanzniveau.
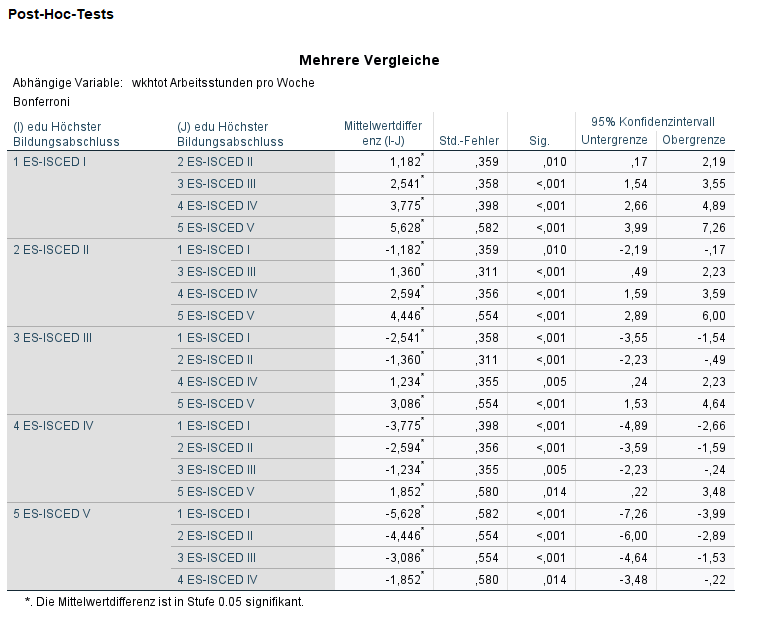
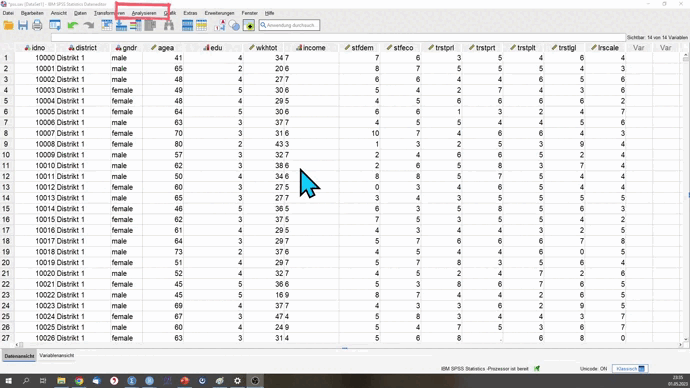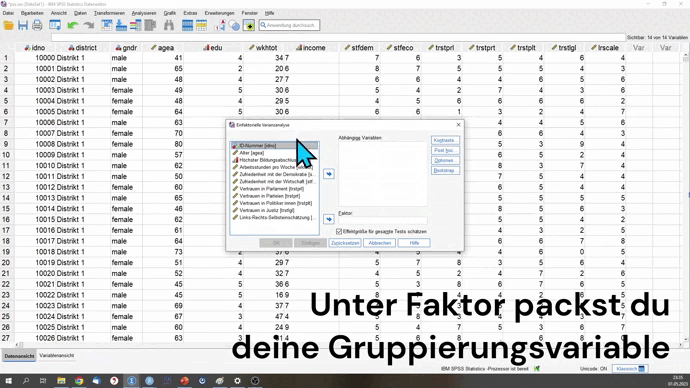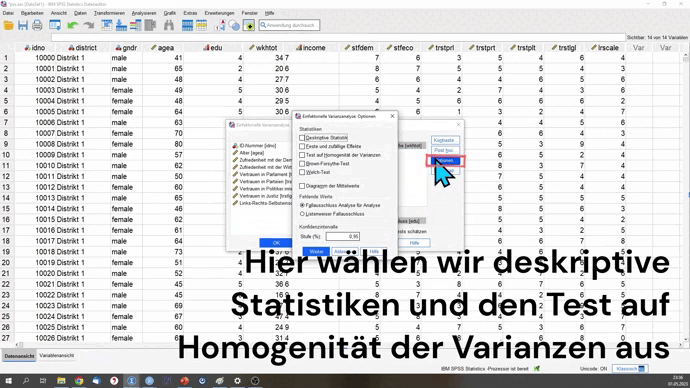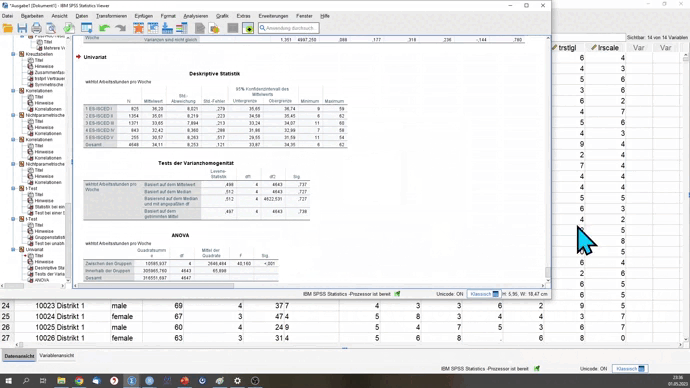
Im Testergebnis siehst du jetzt zusätzlich eine Matrix zwischen den Gruppen, in der die p-Werte für den jeweiligen Vergleich zweier Gruppen eingetragen sind.
So jetzt kannst du nicht nur Zusammenhänge ausgeben lassen, sondern auch Gruppen vergleichen. Das war’s für diesen Lernblock!