Ein-Stichproben-T-Test
Mittelwerte vergleichen
Die zweite große Säule der Datenanalyse ist die Untersuchung von Unterschieden. Dabei werden Mittelwerte zweier oder mehrerer Gruppen verglichen. Dafür wird eine metrische Variable nach einer kategorialen Variable analysiert. So können wir untersuchen, ob eine bestimmte Populationsgruppe systematisch über andere Werte verfügt als eine andere Gruppe. Es gibt mehrere Arten des Mittelwertvergleiches. Diese haben je nach Stichprobenart und Variablenart unterschiedliche Charakteristika. Wir lernen in diesem Abschnitt folgende kennen:
den Ein-Stichproben-t-Test,
den Zwei-Stichproben-t-Test und
den F-Test, auch ANOVA genannt.
Zur Erinnerung: Interpretation der Mittelwertvergleiche
Bei einem Mittelwertvergleich werden immer zwei Hypothesen aufgestellt.
Die Hypothese \(H_1\) nimmt immer an, dass es einen Unterschied zwischen den Mittelwerten bei den Gruppen gibt.
Die Hypothese \(H_0\), oder auch Nullhypothese, nimmt immer das Gegenteil an, also dass es keinen Unterschied zwischen den Mittelwerten bei den Gruppen gibt.
Wir gehen immer dann von einem Mittelwertunterschied aus, wenn wir die Nullhypothese \(H_0\) verwerfen können. Dafür müssen wir sicherstellen, dass der Unterschied zwischen den Gruppen so groß ist, dass wir nicht mehr vom Zufall ausgehen müssen. Dafür gibt es das Signfikanzmaß. Dieses bemisst die Irrtumswahrscheinlichkeit, dass die Nullhypothese falsch ist. Ist die Irrtumswahrscheinlichkeit unter einer vorher festgelegten Minimalgrenze, meistens sind das \(5%\) (\(p < 0.05\)), können wir sagen, dass wir mit großer Sicherheit keinen Irrtum haben, wenn wir die Nullhypothese falsifizieren. Und wenn die Nullhypothese mit großer Sicherheit falsch ist, können wir von einem Mittelwertunterschied zwischen den Gruppen, der kein Zufall ist, ausgehen.
Ein-Stichproben-t-Test
Der Einstichproben-t-Test wird berechnet, um zu testen, ob der empirische Wert signifikant vom wahren Wert \(\mu\) abweicht. Dabei wird der Mittelwert einer Variable aus dem Datensatz mit einem bekannten Mittelwert \(\mu\) verglichen. Die erste Gruppe ist also deine Variable im Datensatz. Diese wird mit dem Mittelwert einer zweiten Gruppe, die extern ist, verglichen.
Du benötigst also Kenntnisse über \(\mu\). Nimm dafür an, dass das Statistikamt das offizielle Durchschnittsalter mit \(36.8\) Jahren angibt.
Welchen Wert nimmt das arithm. Mittel des Alters in unserem Datensatz an?
Die Variable des Alters heißt agea.
T-TEST
/TESTVAL=36.8
/VARIABLES=agea.T-TEST ist der Hauptbefehl. Unter /TESTVAL kannst du das bekannte \(\mu\) eingeben. Nach /VARIABLES definieren wir die Testvariable.
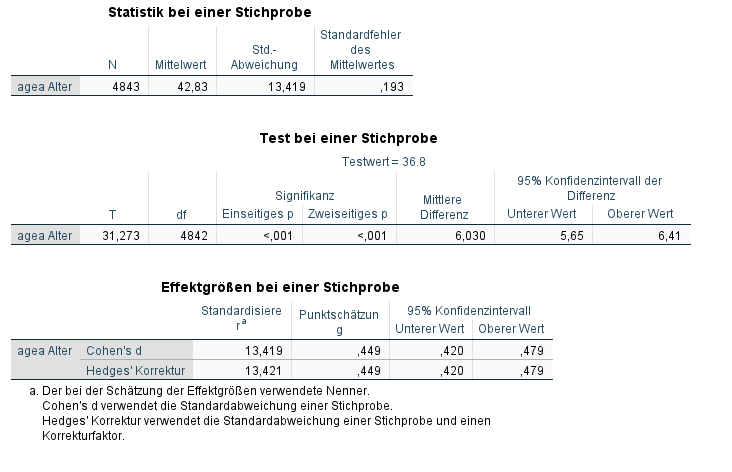
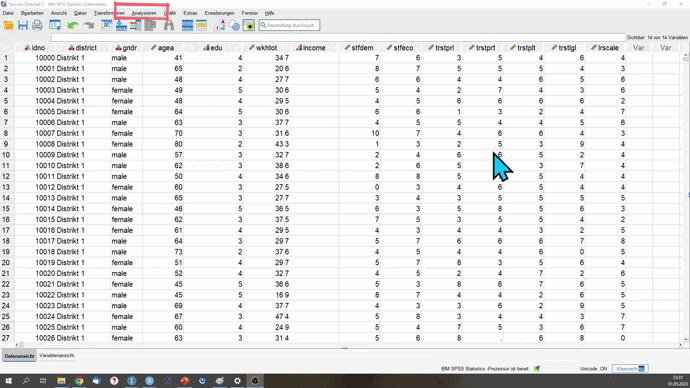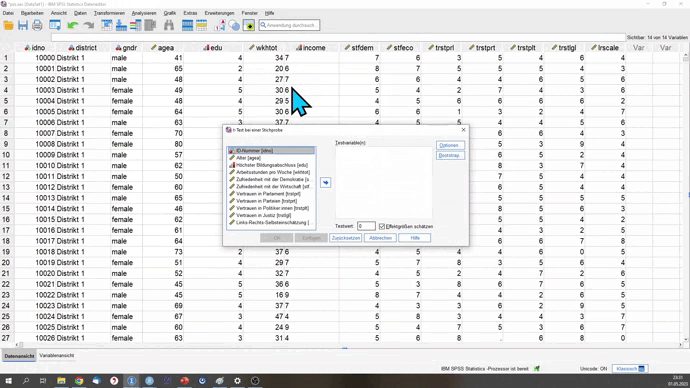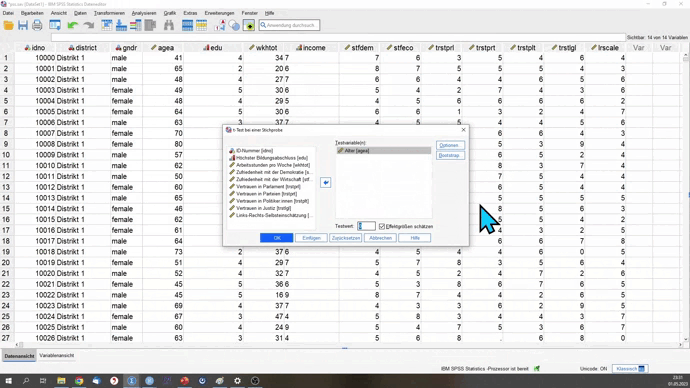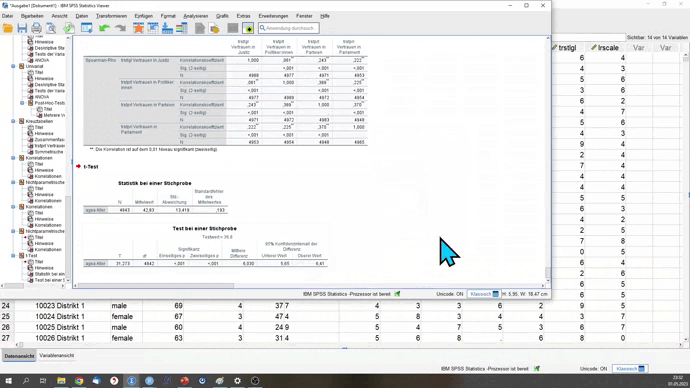
Die wichtigste Teiltabelle ist die Test bei einer Stichprobe. Zum einen sehen wir hier die Mittlere Differenz. Das ist der Unterschied zwischen \(\mu\) und dem Durchschnitt von agea. Der Mittelwert der Stichprobe liegt also um knapp 6 Jahre höher (\(agea_{Stichprobe} = 42.83\)). Diese Abweichung ist signifikant (\(p < 0.05\)).
Gehen wir über zum t-Test für zwei Stichproben!