Zusammenhangsmaße
Mit Zusammenhangsmaßen kannst du testen, ob und inwieweit zwei Variablen miteinander zusammenhängen. Als ein erstes Maß hast du in der Statistik-Vorlesung \(\chi^2\) kennengelernt, das prüft, ob ein Zusammenhang zwischen zwei Variablen vorliegt. Als weiteres Maß für die Stärke eines Zusammenhangs kennst du Cramer’s V. Für die Berechnung der beiden Zusammenhangsmaße betrachten wir den Vergleich zwischen beobachten und erwarteten Werten.
Beobachtete Werte sind die Werte, die gemessen worden sind. Erwartete Werte sind die Werte, die wir erwarten, wenn kein Zusammenhang zwischen den beiden Variablen besteht. Was das genau ist, kannst du hier nachschauen.
CROSSTABS
/TABLES=edu BY gndr
/CELLS=COUNT EXPECTED
Im Unterbefehl /CELLS können wir auch erwartete Werte anzeigen. EXPECTED ist der Parameter für die erwarteten Werte
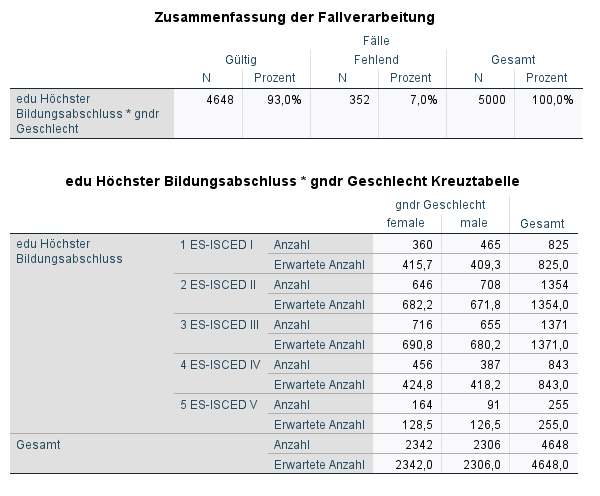
In diesem Output siehst du nicht nur die beobachteten Werte unter Anzahl, sondern auch die erwarteten Werte unter erwartete Anzahl
Aus der Abweichung der beobachteten Werte, also das was wir gemessen haben, und den erwarteten Werten, können wir auf statistische Abhängigkeit vermuten. Dieser Test auf einen Zusammenhang wird mit dem \(\chi^2\)-Unabhängigkeitstest berechnet. Schauen wir uns diesen zuerst an.
\(\chi^2\)-Unabhängigkeitstest
Der \(\chi^2\)-Unabhängigkeitstest gibt Auskunft, ob die ungleiche Verteilung statistisch signfikant ist.
Die Nullhypothese des \(\chi^2\)-Unabhängigkeitstest lautet:
- \(H_0:\) Variablen sind statistisch unabhängig.
Ist das Signfikanzmaß unter einen gewissen Wert, meistens sind das 5%, können wir mit ziemlich großer Sicherheit den Irrtum ausschließen, wenn wir diese Hypothese verwerfen. Oder kurz: Dann können wir von einem statistischen Zusammenhang zwischen den Variablen ausgehen.
CROSSTABS
/TABLES=edu BY gndr
/STATISTICS=CHISQ
/CELLS=COUNT EXPECTED
Ein neuer Unterbefehl ist dazu gekommen /STATISTICS. Nach diesem Befehl können wir mit verschiedenen Parameter statisistische Maßzahlen anfordern, mit CHISQ zum Beispiel \(\chi^2\).
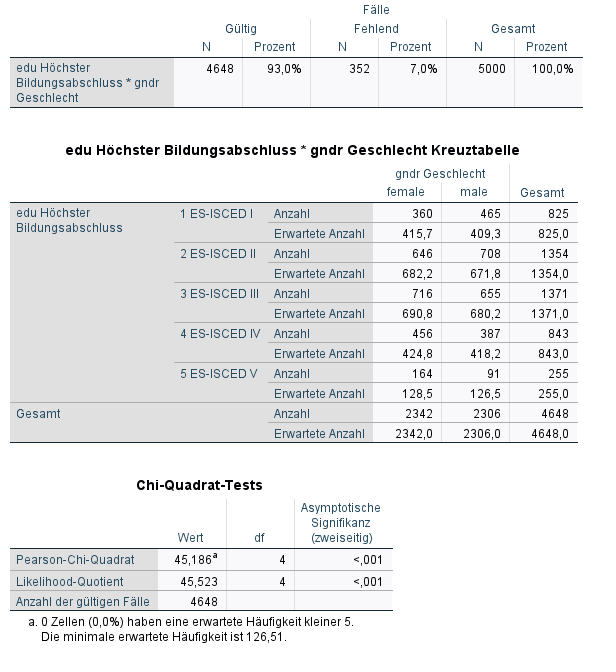
Neu ist hier die Tabelle Chi-Quadrat-Tests. Wir stellen Fest, dass \(\chi^2\) größer als 0 ist. Es liegt also ein Unterschied zwischen den beobachteten und den erwarteten Häufigkeiten. Darüberhinaus ist \(p<0.001\): Mit einer Irrtumswahrscheinlichkeit \(<0.1%\) (also statistisch signifikant auf einem \(0.1%\) Niveau) können wir die Aussage treffen, dass das Geschlecht ungleich über den Schulabschluss verteilt ist.
Annahmen des \(\chi^2\)-Unabhängigkeitstest
Die Berechnung des \(\chi^2\)-Unabhängigkeitstest setzt zwei Annahmen voraus:
- Mindestens \(10\) Beobachtungen in jeder Zelle.
\(\Rightarrow\) Kreuztabelle! (\(\checkmark\))
- Mindestens \(5\) erwartete Beobachtungen in jeder Zelle.
Der \(\chi^2\)-Wert stellt die Summe der Quadrate der standardisierten Residuen dar, die über alle Felder der Kreutzabelle gebildet werden.
Wenn \(\chi^2\) den Wert Null hat, besteht kein Unterscheid zu den erwarteten Häufigkeiten.
Der \(\chi^2\)-Test rechnet zusätzlich einen Signifikanzwert aus. Dieser drückt die Wahrscheinlichkeit aus, einen Fehler erster Art zu begehen: Also die Ablehnung der Nullhypothese, obwohl diese wahr ist. Die Konvention liegt bei \(5%\) und daher werden Ergebnisse mit \(p < 0.05\) als signifikant bewertet, da hier der Fehler \(<=5% (0.05)\) ist.
Die Stärke des Zusammenhangs
Bisher haben wir nur den \(\chi^2\)-Unabhängigkeitstest durchgeführt. Aber neben dem generellen Zusammenhang ist oftmals von Interesse, wie stark dieser Zusammenhang ist bzw. in welche Richtung dieser Zusammenhang geht. Dafür gibt es weitere Maßzahlen. Aufgrund der mathematischen Eigenschaften der verschiedenen Skalenniveaus, gibt es je Skalenniveau unterschiedliche Zusammenhangsmaße.
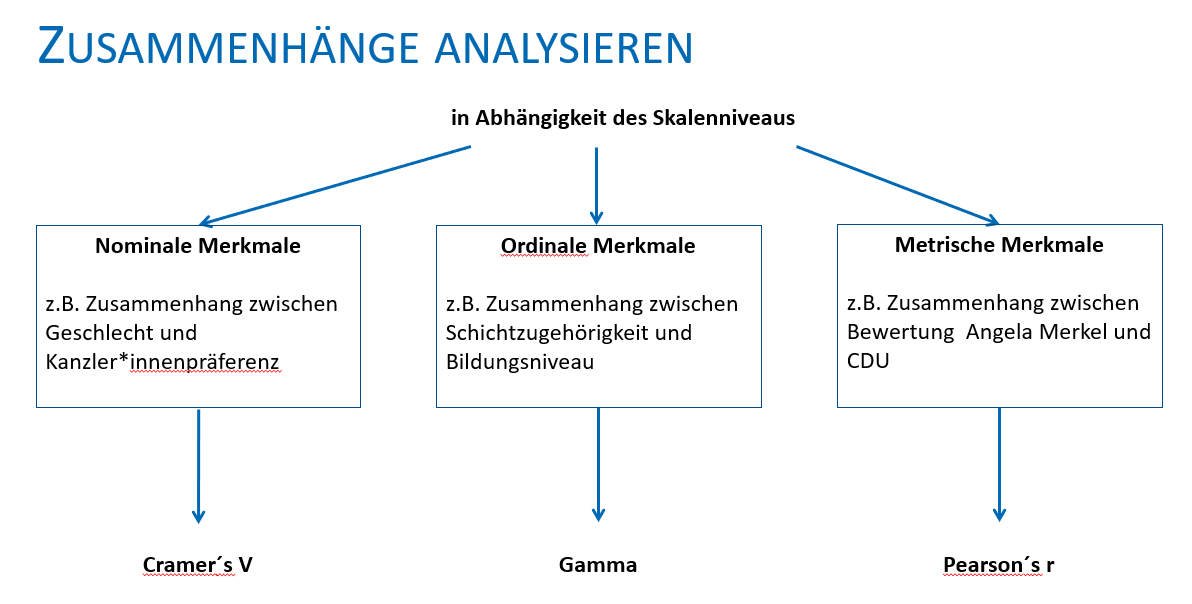
Für den Zusammenhang zwischen nominalen Variablen nutzen wir Cramer’s V.
Für den Zusammenhang zwischen ordinalen Variablen nutzen wir Gamma.
Für den Zusammenhang zwischen metrischen Variablen nutzen wir Pearson’s R.
Cramer’s V
Wir berechnen Cramer’s V für die Stärke des Zusammenhangs zwischen zwei mindestens nominalskalierten Variablen. Cramer’s V:
nimmt Werte zwischen 0 und 1 an,
und gibt uns die Stärke eines Zusammenhanges aus.
Also genau das, was wir mit \(\chi^2\) nicht machen konnten, super!
Für die Interpretation der Stärke des Zusammenhanges gelten folgende Grenzen:
| unteres Ende | oberes Ende | Interpretation |
|---|---|---|
| \(0\) | \(0.1\) | kein Zusammenhang |
| \(0.1\) | \(0.3\) | gering |
| \(0.3\) | \(0.6\) | mittel |
| \(0.6\) | \(1\) | stark |
CROSSTABS
/TABLES=edu BY gndr
/STATISTICS=CHISQ PHI
/CELLS=COUNT EXPECTED
Mit dem Parameter PHI fordern wir Cramer’s V an. \(\phi\) (Phi) ist ein Spezialfall von Cramer’s V auf 2x2 Kreuztabellen.
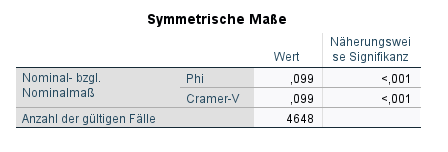
Cramer’s V beträgt \(0.099\). Es liegt also ein sehr schwacher Zusammenhang vor, der auf \(0.1%\) Niveau signifikant ist.
Gamma
Als nächstes ist Gamma an der Reihe. Für die Berechnung von Gamma benötigst du mindestens ordinalskalierte Variablen. Gamma hat eine andere Konzeption als Cramer’s V. Für Gamma gilt:
Es nimmt Werte zwischen 0 und 1 an,
gibt die Stärke eines Zusammenhanges aus
und gibt die Richtung des Zusammenhanges an.
Letzteres bedeutet, dass unsere Werte nun ein Vorzeichen beinhalten. Ist
\(\gamma\) = +1, handelt es sich um einen perfekten positiven Zusammenhang,
\(\gamma\) = 0, handelt es sich um keinen Zusammenhang,
-* \(\gamma\) = -1, handelt es sich um einen perfekten negativen Zusammenhang.
Positive Werte bedeuten, dass ein hoher (numerischer) Wert bei der einen Variable mit einem hohen (numerischen) Wert bei der anderen Variable korresponidert. Negative Werte bedeuten, dass ein hoher (numerischer) Wert bei der einen Variable mit einem niedrigen (numerischen) Wert bei der anderen Variable korresponidert.
Zusätzlich erhalten wir ebenfalls einen Signfikanzwert. Schauen wir uns an, wie das in SPSS funktioniert.
Für dieses Beispiel nehmen wir zwei ordinal-skalierte Variablen: Das Einkommen in Dezilen und den Schulabschluss.
CROSSTABS
/TABLES=income BY edu
/STATISTICS=CHISQ GAMMA
/CELLS=COUNT EXPECTED
Mit dem Parameter GAMMA fordern wir \(\gamma\) an.

Gamma beträgt \(0.527\). Es liegt also ein mittlerer Zusammenhang vor, der auf \(0.1%\) Niveau signifikant ist.
Super, die ersten beiden Zusammenhangsmaße hast du geschafft, machen wir jetzt mit Pearson’s R weiter!