Beobachtete und erwartete Häufigkeiten
Mit Kreuztabellen wird versucht, die Unabhängigkeit von Variablen zu prüfen. Bei Unabhängigkeit muss die prozentuale Verteilung der abhängigen Variablen in jeder Ausprägung der unabhängigen Variable gelten. Im Beispiel hieße es, dass sowohl auf dem Land als auch in der Stadt die Aufteilung zwischen Wahl der CDU und Nicht-Wahl der CDU gleich der Gesamtaufteilung ist.
Abweichungen von diesen Verteilungen lassen darauf schließen, dass die Variablen nicht unabhängig voneinander sind. Wenn die Variablen nicht unabhängig voneinander sind, wird dies als Zusammenhang gewertet.
Aus diesem Grund werden immer auch die relativen beobachteten Häufigkeiten der Kombination angegeben. In der Konvention werden die Prozente in Abhängigkeit der Spalte dargestellt. Für jede Spalte wird die prozentuale Häufigkeit berechnet.
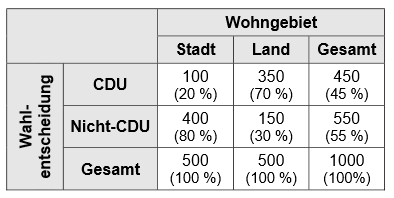
Von den in der Stadt lebenden Personen haben also 20 % CDU gewählt und von Personen, die auf dem Land leben 70 %. Anhand der beobachteten Häufigkeiten lassen sich deutlich unterschiedliche Präferenzen für Personen erkennen, die auf dem Land leben und Personen, die in der Stadt leben.
Um diesen Befund nun statistisch zu prüfen, muss zuerst eine Indifferenztabelle berechnet werden. Diese Indifferenztabelle nimmt die erwarteten Werte an, wenn kein Zusammenhang zwischen den Variablen besteht. Das heißt, in beiden Spalten der unabhängigen Variable müssten die gleichen Häufigkeiten wie in der Gesamtverteilung stehen.
Wenn kein Zusammenhang bestehen würde, ergibt sich somit die gleiche prozentuale Verteilung. Das Rechenbeispiel finden Sie auch in einem Lernvideo auf der nächsten Seite. Die erwartete Häufigkeit bei Unabhängigkeit, die sogenannte Indifferenztabelle, ergibt sich aus der beobachteten Randverteilung: Wir wissen aus den Daten, dass insgesamt 45 % CDU gewählt haben und 55 % nicht die CDU gewählt haben. Dies ist in der letzten Spalte oben zu sehen. Alternativ errechnet sich die erwartete Häufigkeit wie folgt:
\(f_{e_{ij}}=\frac {f_{e_{i.}} \ast f_{e_{.j}}}{n}\), wobei gilt das \(f_{e_{i.}}=Zeilensumme\) und \(f_{e_{.j}}=Spaltensumme\) ist.
Im Beispiel ergibt sich die Ausprägung Wahl der CDU folgende erwartete Häufigkeit:
\[\begin{align*}f_{e_{ij}}&=\frac {f_{e_{i.}} \ast f_{e_{.j}}}{n} \\ &=\frac{450 \ast 500}{1000} \\ &= \frac{22500}{1000} \\ &= 225 \end{align*}\]
Liegt Unabhängigkeit vor, muss dieses Verteilungsmuster auch in den einzelnen Spalten der abhängigen Variable vorliegen. Daraus ergibt sich dann die Indifferenztabelle.
Die Werte der folgenden Tabelle würden wir bei Unabhängigkeit erwarten, deshalb bezeichnet man diese auch als erwartete Werte im Gegensatz zu den beobachteten Werten zuvor. Diese Tabelle stellt eine Indifferenztabelle dar.
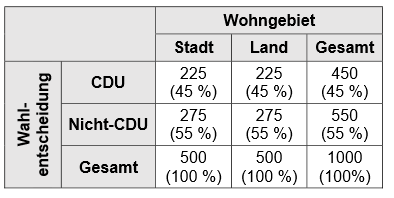
Aus der Differenz zwischen der Kontingenztabelle mit den beobachteten Werten und der Indifferenztabelle mit den erwarteten Werten wird der Zusammenhang dann überprüft.
Siehe auch: Gehring & Weins (2009, Kapitel 7.1).
Im folgenden Lernvideo wird Ihnen an zwei Beispielen die Berechnung der erwarteten Werte dargestellt.