Normalverteilung
Die Normalverteilung ist das wichtigste Verteilungsmodell der Statistik und wird für verschiedene Zwecke verwendet. Die Normalverteilung ist eine Verteilungsfunktion stetiger Variablen. Die Normalverteilung ist relevant als Verteilung empirischer Merkmale, als Verteilung von Stichprobenkennwerten und als Approximation anderer theoretischer Verteilungen (zentraler Grenzwertsatz, dazu im nächsten Kapitel mehr).
Die Normalverteilung wird auch als Gauß-Verteilung beschrieben, da sie auf Carl Friedrich Gauß und Abraham de Moivre zurückgeht. Aufgrund der charakteristischen Form wird sie vereinfacht auch Glockenkurve genannt. Das Maximum einer Normalverteilung liegt dabei immer im Erwartungswert \(\mu\) und die Fläche unterhalb der Kurve der Normalverteilung ist stets 1 (im Intervall \([-\infty; +\infty]\)). Die Dichtefunktion der Normalverteilung lautet: \(f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}\).
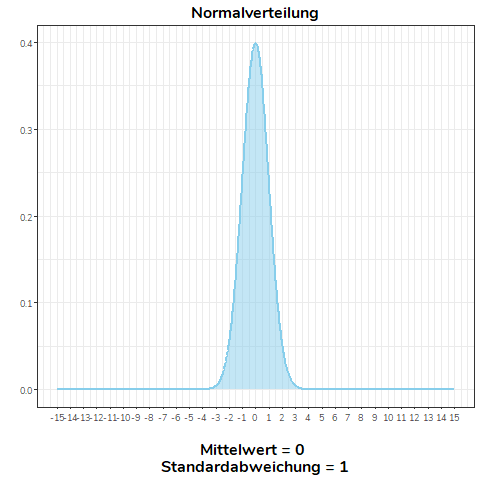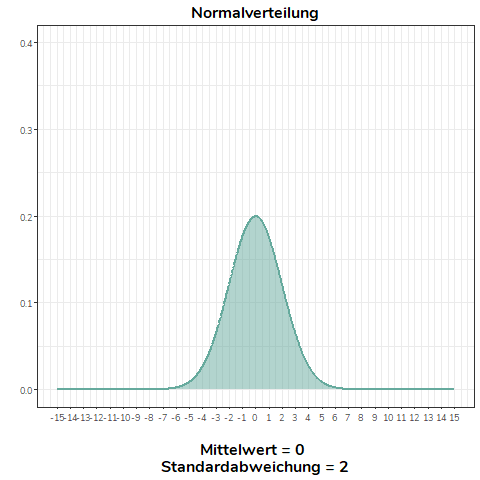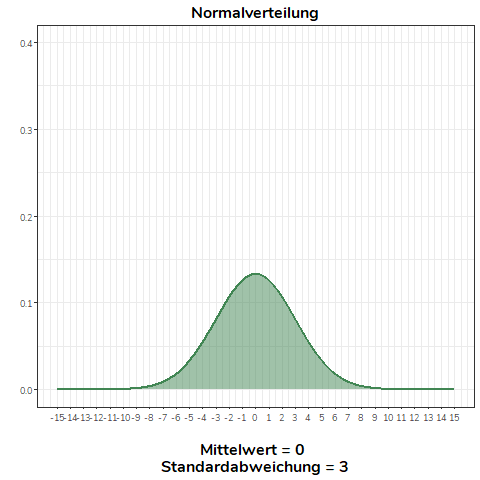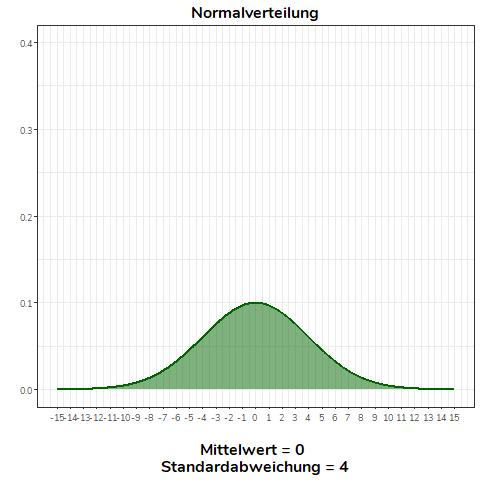
Eine Normalverteilung mit \(\bar{x}=0, \sigma=1\) entspricht daher folgender Abbildung:

Auf der \(y\)-Achse ist dabei die Häufigkeit abgetragen und auf der \(x\)-Achse die Werte einer Verteilung. Wie zu erkennen ist, teilt der Erwartungswert die Verteilung genau in der Hälfte und stellt auch den Modus, Mittelwert wie Median dar. Die Normalverteilung ist daher unimodal und symmetrisch.
Ändert sich der Mittelwert der Normalverteilung, verschiebt sich diese nach links (\(\bar{x}<0\)) bzw. nach rechts (\(\bar{x}>0\)). Alle Normalverteilungen im Beispiel haben die selbe Standardabweichung (\(\sigma=1\)).
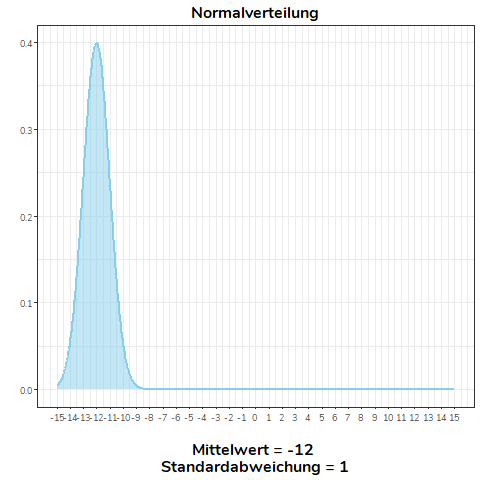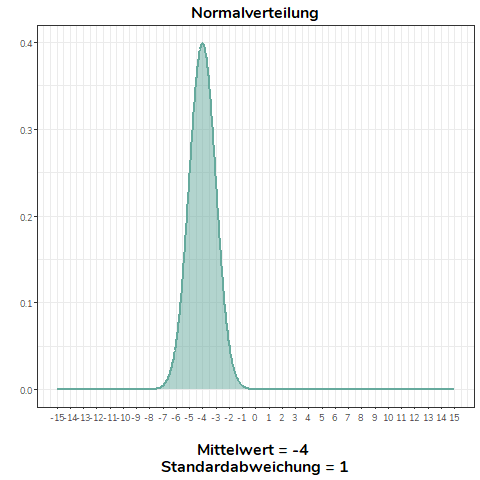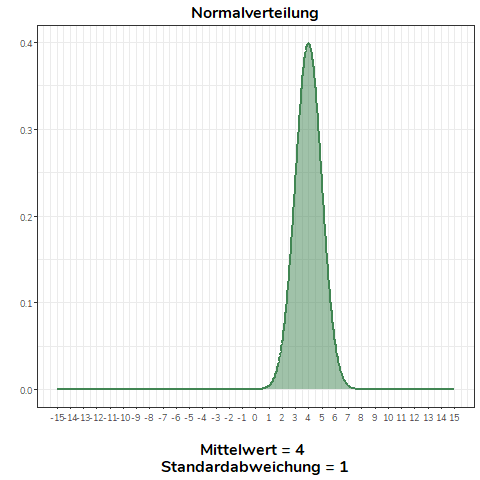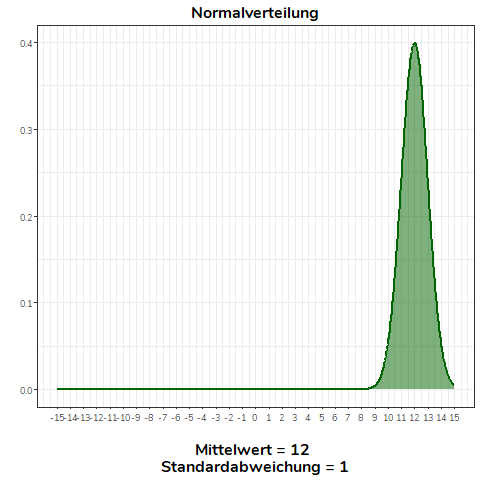
Ändern wir nicht den Mittelwert, sondern die Standardabweichung einer Normalverteilung, wird diese flacher (\(\sigma>1\)) bzw. steiler (\(0<\sigma<1\)). Für alle Normalverteilungen in diesem Beispiel gilt \(\mu = 0\).
Die Normalverteilung hat in statistischen Tests eine wichtige Stellung. In statistischen Tests wird berechnet, wie wahrscheinlich ein Wert sich innerhalb eines Intervalls befindet und somit als „wahrscheinlich“/signifikant angenommen werden kann. Dazu wird über die Dichtefunktion der Normalverteilung die Verteilungsfunktion gebildet, so dass für Intervalle Wahrscheinlichkeiten berechnet werden können. Dazu ist es wichtig, die Verteilungsregel der Normalverteilung zu verinnerlichen. Für die Normalverteilung sind dabei folgende wichtige Flächen festzuhalten anhand der Standardabweichung festzuhalten.

Bei einer Normalverteilung sind fast alle Werte innerhalb von drei Standardabweichungen erreicht.
Dies verdeutlicht die obere Grafik: Innerhalb des Intervalls von einer Standardabweichung (\([-1, 0]\)) befinden sich 68 % der Verteilung (\(2*34 %\)). In einem Intervall von +/- 2 Standardabweichungen (\([-2, 2]\)) befinden sich weitere 27 % (\(2*13,5 %\)), also insgesamt 95 %.
Innerhalb eines Intervalls von +/- 3 Standardabweichungen (\([-3, 3]\)) befinden sich weitere 4,7 % (\(2*2,35 %\)), also insgesamt knapp 99,7 %.
Das bedeutet, dass die Wahrscheinlichkeit, dass ein Wert \(x\) innerhalb des ersten Intervalls \([\mu - \sigma, \mu + \sigma]\) liegt, 0.68 beträgt (\(P(\mu - \sigma \leq x \leq \mu + \sigma) \approx 0.68\)).
Für das Intervall \([\mu - 2\sigma, \mu + 2\sigma]\) beträgt die Wahrscheinlichkeit eines Wertes \(x\) knapp 0,95 (\(P(\mu - 2\sigma \leq x \leq \mu + 2\sigma) \approx 0.95\)).
Und innerhalb von drei Standardabweichungen beträgt die Wahrscheinlichkeit, dass ein Wert \(x\) innerhalb dieses Intervalls \([\mu - 3\sigma, \mu + 3\sigma]\) liegt, knapp 0,99 (\(P(\mu - 3\sigma \leq x \leq \mu + 3\sigma) \approx 0.99\)). Nahezu alle Fälle liegen bei einer Normalverteilung innerhalb von drei Standardabweichungen.