Spearman's Rho
Für den Zusammenhang zweier ordinaler Variablen kann man die Rangkorrelation nach Spearman (\(\rho\)) benutzen. Voraussetzung hierfür sind die Monotonie des Zusammenhangs und mindestens ordinale Variablen des Zusammenhangs. Auch kann ein nicht-linearer, aber monotoner Zusammenhang zweier metrischer Variablen mit Spearmans \(\rho\) analysiert werden.
Wie auch der Korrelationskoeffizient nach Pearson nimmt Spearmans \(\rho\) Werte im Intervall \([-1;+1]\) an. Für den perfekt positiven Zusammenhang nimmt er die Maßzahl $+1 $ an, für den perfekt negativen den Wert \(-1\).
Für die Berechnung von Spearmans \(\rho\) müssen zuerst Rangwerte der Variablen \(x\) und \(y\) erstellt werden (\(R(x)\) und \(R(y)\)). Die Datenreihen werden der Größe nach sortiert.
Als Besonderheit gilt bei Spearmans \(\rho\), dass die Abstände äquidistant (wie bei metrischen Variablen) sein müssen. Es muss also gewährleistet sein, dass die Rangdifferenzen tatsächlich die inhaltlichen Differenzen abbilden.
Für die Berechnung von geteilten Rängen werden Durchschnittsränge ermittelt. Sollte der Wert \(1\), die 1., 2. und 3. Position beinhalten, wäre der Rang für die drei Merkmalsausprägungen mit dem Wert \(1\) folgender: \(Rang = \frac {1} {3} \ast (1+ 2 +3) = 2\) . Anstatt des Mittelwertes wird in der Berechnung von Spearmans \(\rho\) der Durchschnittsrang verwendet: \(\bar{R(x)}\) oder \(\bar{R(y)}\)
Für die Berechnung kann eine vereinfachte Formel herangezogen werden. Hier werden die wahren Werte durch die Rangwerte ersetzt, und mit diesen Rangwerten erfolgt die Berechnung der Rangkorrelation. Die Berechnung von Spearmans \(\rho\) beruht daher nur auf der Ordnung der Daten (\(>\), \(<\)).
Die vereinfachte Formel zur Berechnung von Spearman´s \(\rho\):
\(\rho = 1 - \frac {6 \ast \sum\limits_{i=1}^n d^2_i}{n \ast (n^2 -1)}\), wobei \(d_i = R(x_i) - R(y_i)\) ist.
Diese Formel gilt nur, wenn keine Rangbindungen auftreten oder höchstens 20 Prozent der Paare Rangbindung haben.
Beispiele
Sie können nun anhand zweier Beispiele (einmal im Lernvideo und ein weiteres unten im Text) die Berechnung der Spearman-Korrelation nachvollziehen.
Nehmen wir ein weiteres Beispiel: Wir messen die Note von Studierenden einer Statistik-Vorlesung. Wir wollen testen, inwieweit die Endnote (\(x\)) mit der Note des Zwischentests (\(y\)) korreliert. Da es sich um eine Beispielrechnung handelt, erheben wir zum leichteren Verständnis nur Daten von fünf Studierenden (ohne Rangbindung).
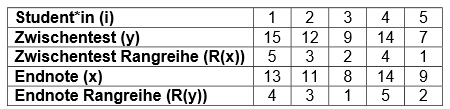
Diese Daten übertragen wir nun in eine geordnete Tabelle der Rangreihen und extrahieren daraus die sortierte Rangreihe nach der Endnote (\(R(x_i)\)). Hierbei benötigen wir nur noch die Rangreihen und nicht mehr die eigentlichen Notenpunkte im Zwischen- bzw. Endtest.
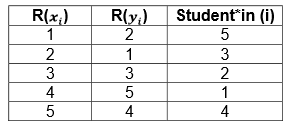
Diese Daten müssen wir nun einfach in unsere vereinfachte Formel einsetzen: \(\rho = 1 - \frac {6 \ast \sum\limits_{i=1}^n d^2_i} {n \ast (n^2 - 1)}\), wobei \(d_i = R(x_i) - R(y_i)\) ist.
\[ \begin{align*} \rho &= 1 - \frac {6 \ast [(1-2)^2 + (2-1)^2 + (3-3)^2 + (4-5)^2 + (5-4)^2]} {5 \ast (5^2 -1)} \\ &= 1- 0.2 \\ &= 0.8 \end{align*}\]
In unserer Beispielrechnung erhalten wir ein \(\rho = 0,8\). Die Endnote korreliert folglich sehr stark mit der Note des Zwischentests. Interpretativ heißt dies, dass Personen, die bereits im Zwischentest eine gute Note erreicht haben, auch eine gute Endnote erreicht haben.