Stetige Zufallsvariable
Bei stetigen Variablen können Wahrscheinlichkeiten nicht direkt berechnet werden. Auch die Dichtefunktion liefert im Gegensatz zur Wahrscheinlichkeitsfunktion nicht direkt Wahrscheinlichkeiten. Aber aus der Fläche der Dichtefunktion wird die Wahrscheinlichkeit berechenbar. Die Verteilungsfunktion bei stetigen Variablen ergibt sich durch ein Integral der Dichtefunktion: \(F(x) = P(X \leq x) = \int_{-\infty}^{x} f(x)dx\). Wichtig ist hierbei folgendes: Die Wahrscheinlichkeit, dass die Zufallsvariable \(X\) einen genauen Wert \(x\) annimmt ist gleich 0 (\(P(X=x)=0\), die Fläche unter diesem Teil ist \(0\)). Das kann man ganz einfach aus der Formel ableiten: \(P(X=x) = \int_{x}^{x} f(x) dx= F(x) -F(x) = 0\). Auch hier gilt, dass die Verteilungsfunktion Werte als Gesamtwert \(1\) annimmt (\(F(x) = \int_{-\infty}^{+\infty} f(x)dx = 1\)). Die Dichtefunktion (\(f(x)\)) dagegen ist immer positiv, kann aber auch Werte über \(1\) annehmen (\(f(x)\geq 0\) für alle \(x \in \mathbb{R}\)).
Über die Dichteverteilung erhalten wir einen visuellen Eindruck: Die Darstellung zeigt uns, in welchen Teilen Werte der Zufallsvariablen besonders dicht beianeinander sind. Die Dichtefunktion kann nur positive Werte annehmen (\(f(x) \geq 0\) für alle \(x \in \mathbb{R}\)). Die Wahrscheinlichkeit \(P(X \leq x)\) errechnet sich durch Integration der Dichtefunktion: \(F(x) = P(X \leq x) = \int_{-\infty}^{x} f(x)dx\) (Verteilungsfunktion stetiger Zufallsvariablen). Dabei gilt, dass die Fläche unter der Dichtefunktion (im Gegensatz zur Verteilungsfunktion bei diskreten Variablen) den Inhalt 1 besitzt (\(\int_{-\infty}^{+\infty} f(x)dx = 1\)). Da Integrale nicht so einfach berechenbar sind, wird die Berechnung hier nur grafisch vorgestellt.
Schauen wir uns Beispiele an:
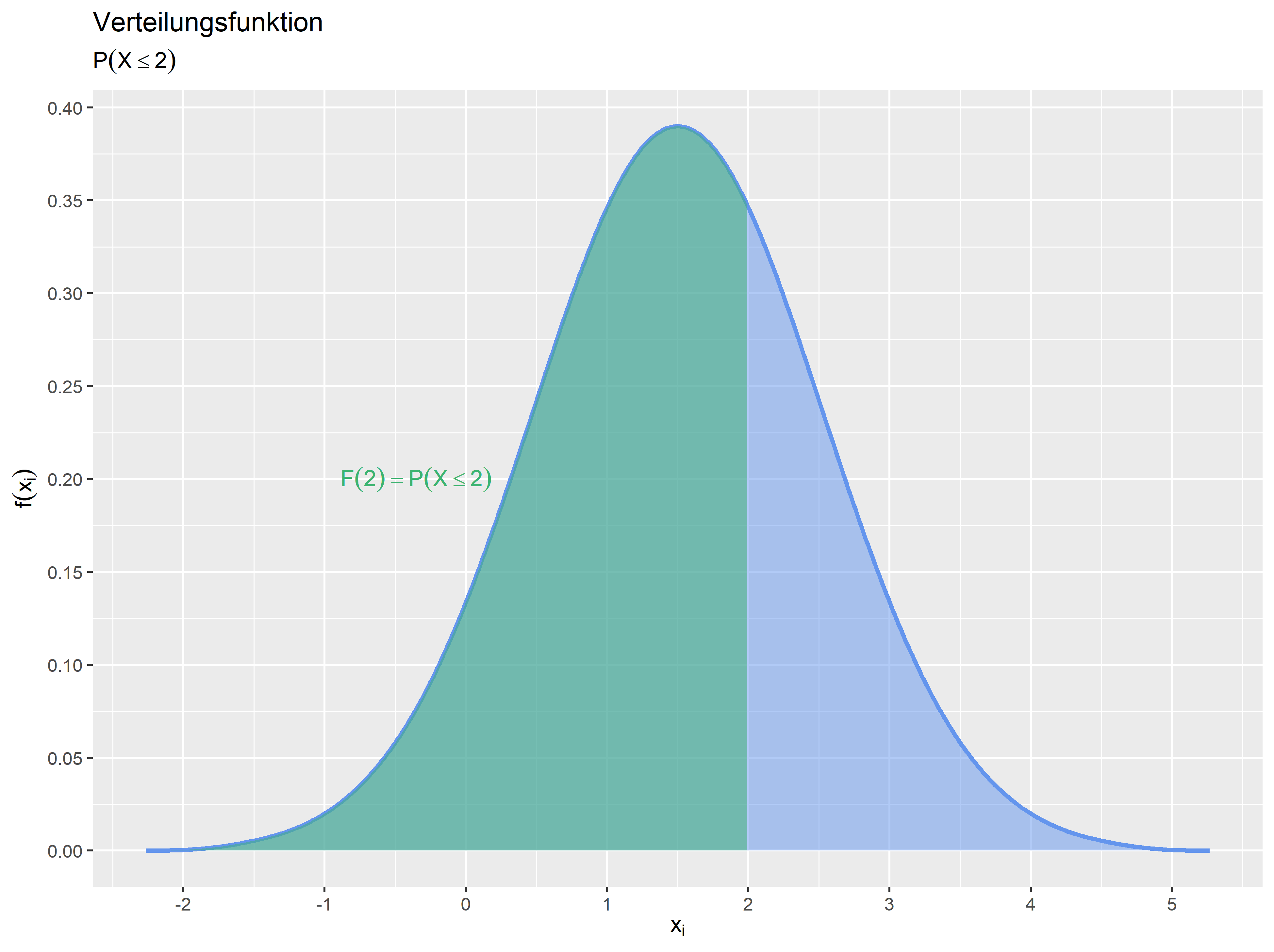
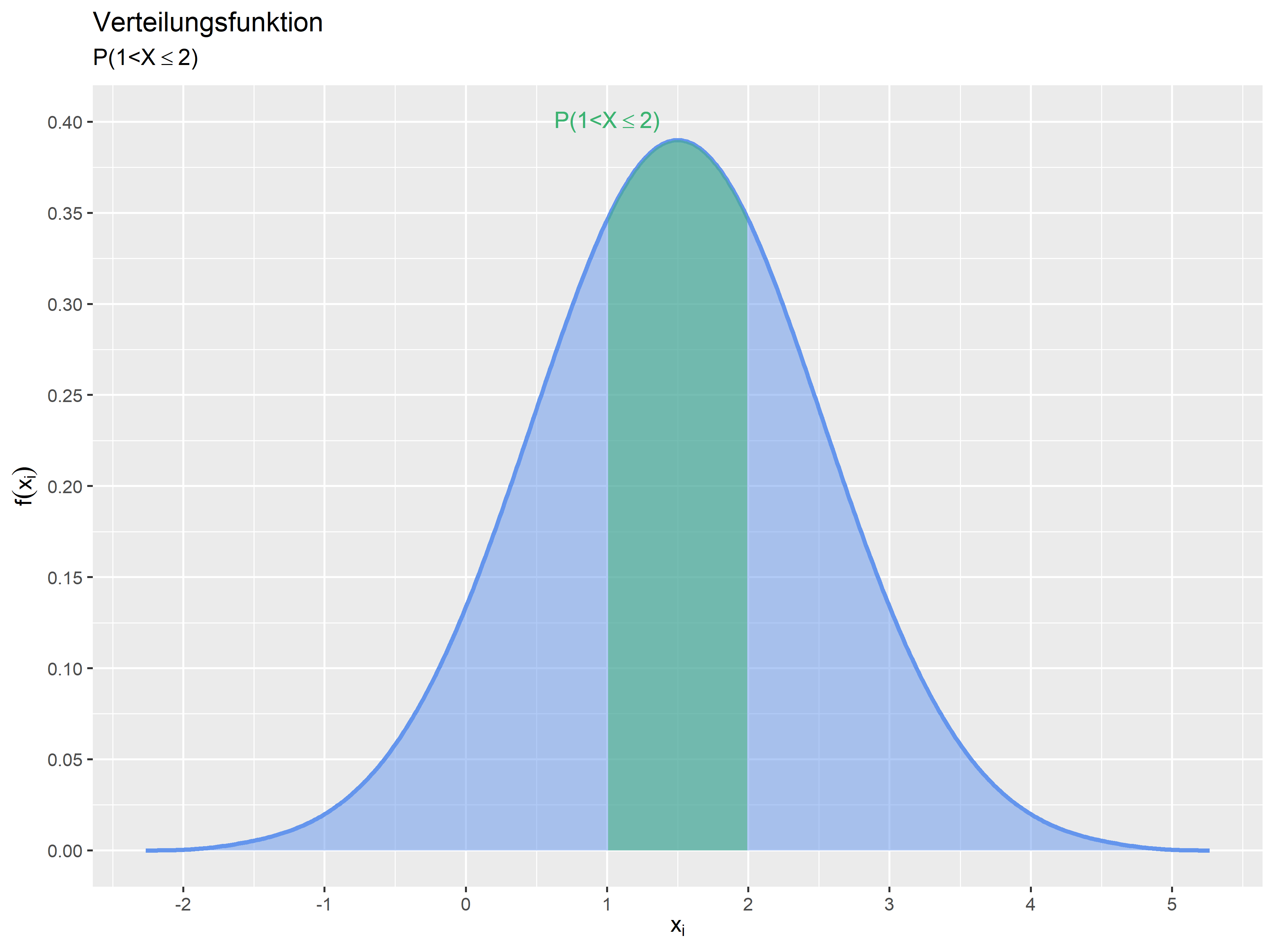
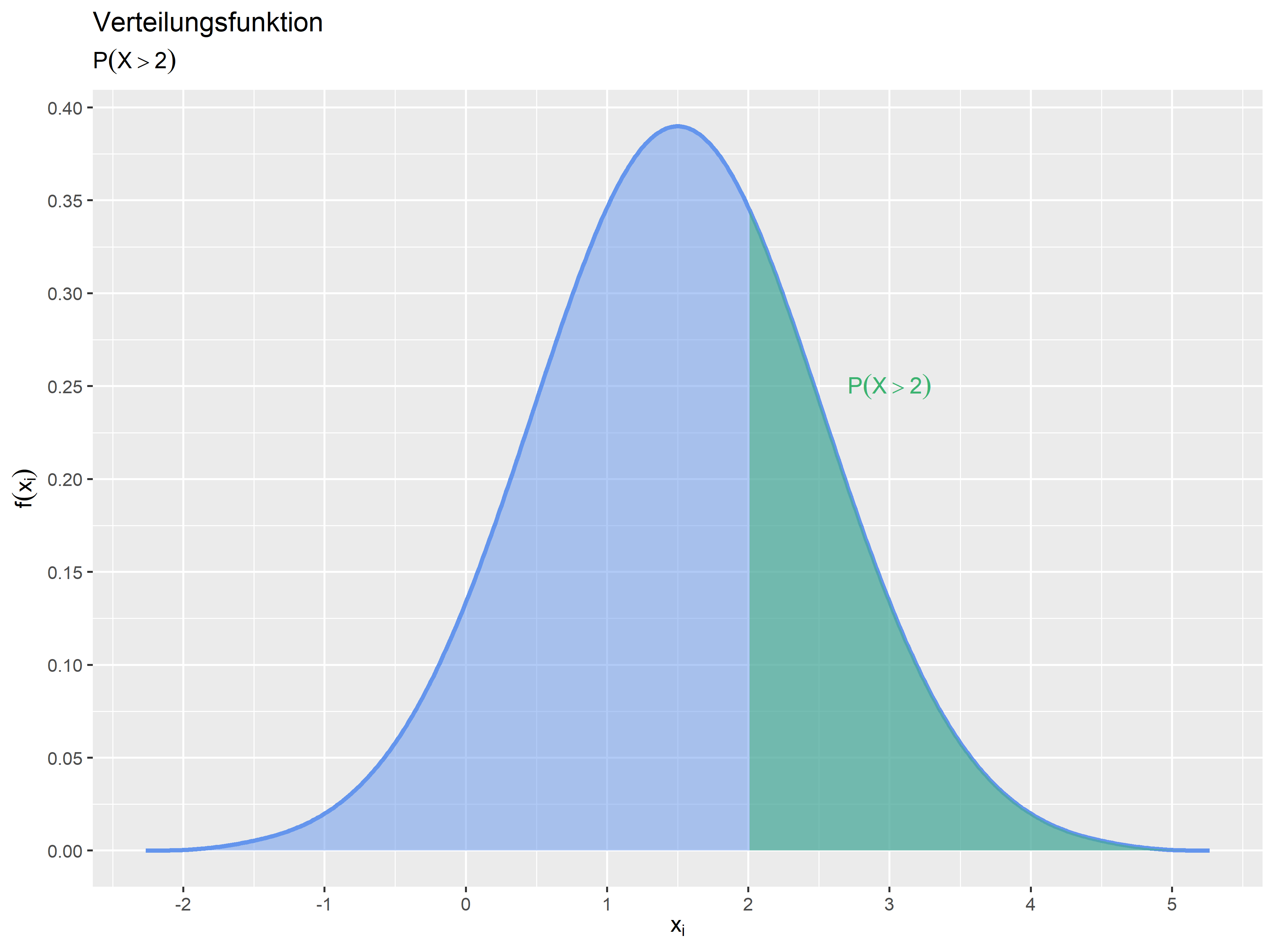
Die Verteilungsfunktion wird zwar meist über die Fläche der Dichtefunktion dargestellt, es kann aber auch die Verteilungsfunktion ausgegeben werden. Hier sehen Sie das Beispiel:
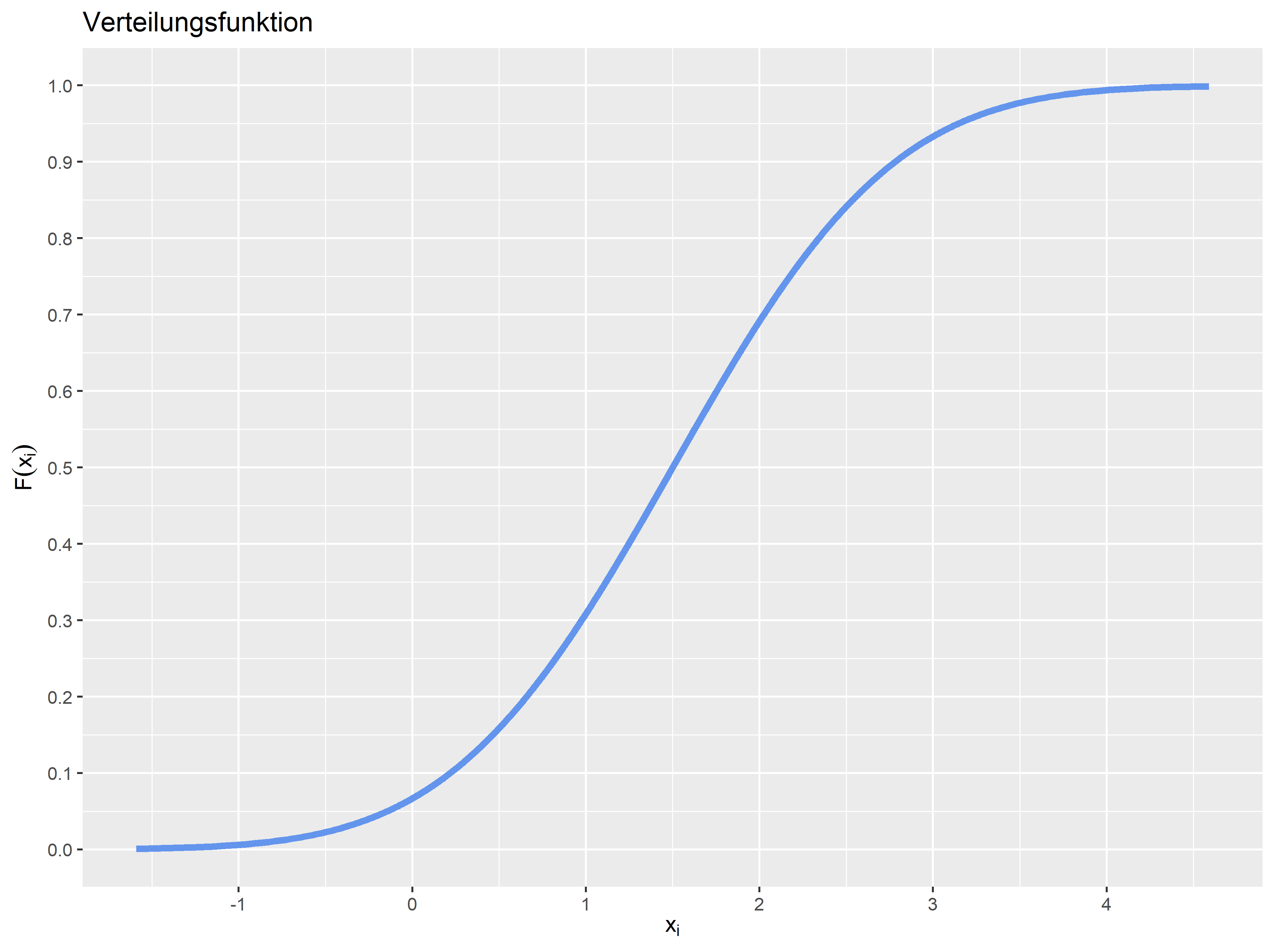
Gegenüber diskreten Variablen gibt es einen immens wichtigen Unterschied. Aus \(F(x) = P(X \leq x) = \int_{-\infty}^{x} f(x)dx\) könne wir folgende Eigenschaft ableiten: \(P(X = x) = 0\). Das heißt, bei stetigen Variablen ist die Wahrscheinlichkeit, dass die Zufallsvariable genau einen bestimmten Wert annimt immer \(0\). Ursache dafür ist, dass die Fläche unter einem Punkt \(x\) gleich Null ist: \(P(X=x) \int_x^x f(x)dx = F(x)- F(x) =0\). Die Wahrscheinlichkeitsfunktoin ist also für stetige Zufallsvariablen nicht definiert.
Im Folgenden werden nun die stetigen Verteilungsfunktionen Normalverteilung, Standardnormalverteilung und t-Verteilung vorgestellt.
Siehe auch: Bortz & Schuster (2010, Kapitel 5.3, 5.4).