Linearität & Monotonie
Bei der Berechnung der Korrelation nach Pearson müssen zwei Bedingungen erfüllt sein: Der Zusammenhang muss linear und monoton sein.
Die folgende Abbildung zeigt einen Scatterplot eines nicht linearen und nicht monotonen Zusammenhangs zweier Variablen. Beides kann auf Sicht in einem Scatterplot erkannt werden. Das Verfahren der Korrelationsberechnung erkennt dies nicht.
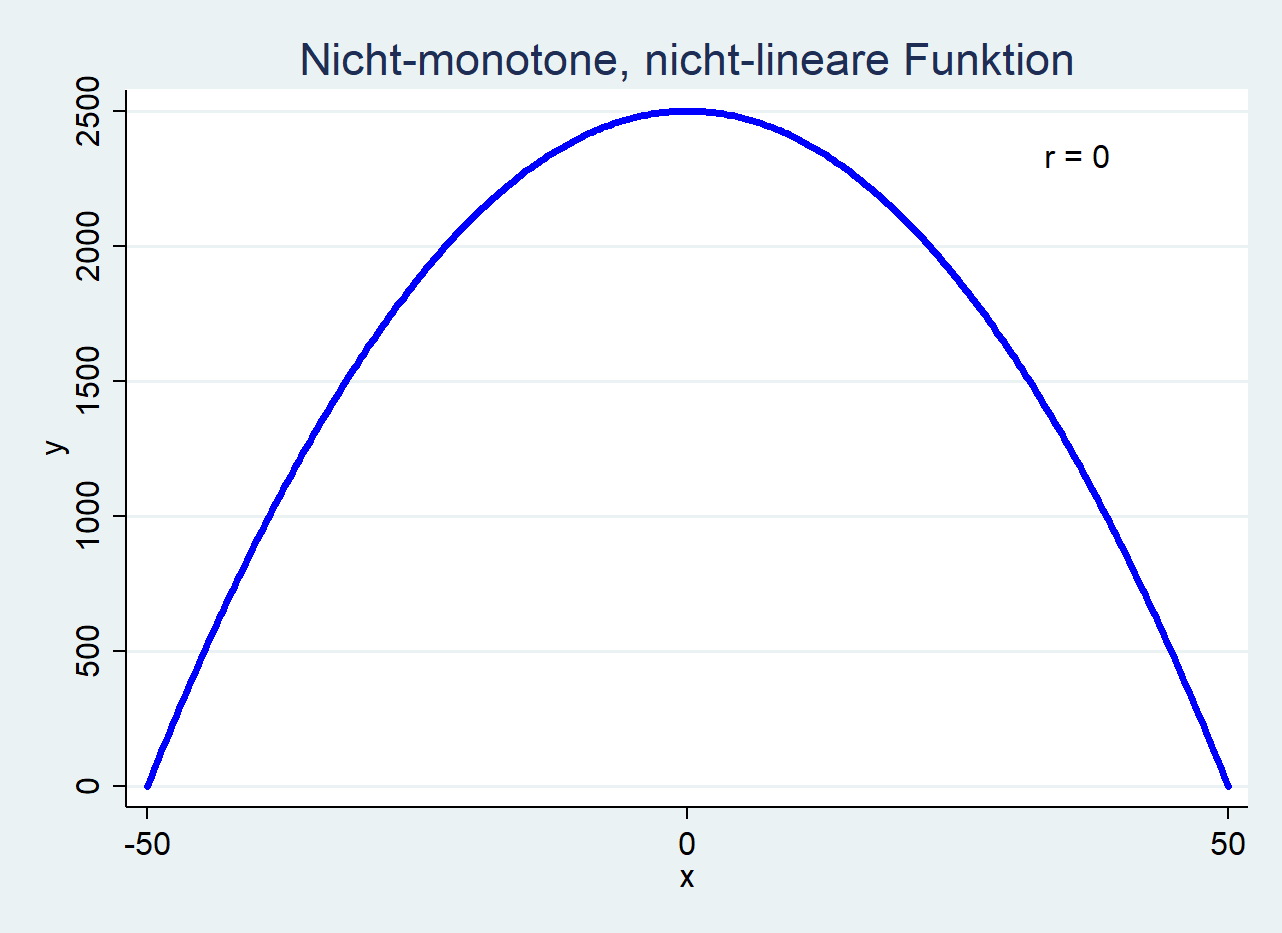
Bis zum \(x\)-Wert \(0\) steigen die \(y\)-Werte und ab dann sinken die \(y\)-Werte für steigendes \(x\) (Nicht-Monotonie, Nicht-Linearität). Die Art der Beziehung zwischen den Variablen verändert sich mit steigendem \(x\) (erst steigt auch \(y\), danach sinkt \(y\)). Die Grundbedingung der Pearson-Korrelation ist nicht gegeben. Dies wird auch deutlich am Wert der Pearson-Korrelation: Dieser wird in diesem Beispiel mit \(r=0\) angegeben. Demnach dürfte kein Zusammenhang zwischen den zwei Variablen vorliegen, aber die Grafik zeigt sehr deutlich, dass ein Zusammenhang vorliegt, der perfekt ist (Punkte bilden eine Linie), aber nicht monoton und nicht linear. So kommt es zu einem falschen Korrelationswert bei der Berechnung der Pearson-Korrelation.
Ein weiteres Beispiel verdeutlicht die Verletzung der Linearität. In der Grafik sehen Sie einen Scatterplot zwischen Nettoeinkommen (offene Abfrage in Euro) und den Arbeitsstunden pro Woche (offene Abfrage). Der ausgegebene Pearson-Korrelationskoeffizient wäre für diese Beispiel bei \(r=0.388\). Damit würde ein schwacher Zusammenhang vorliegen.
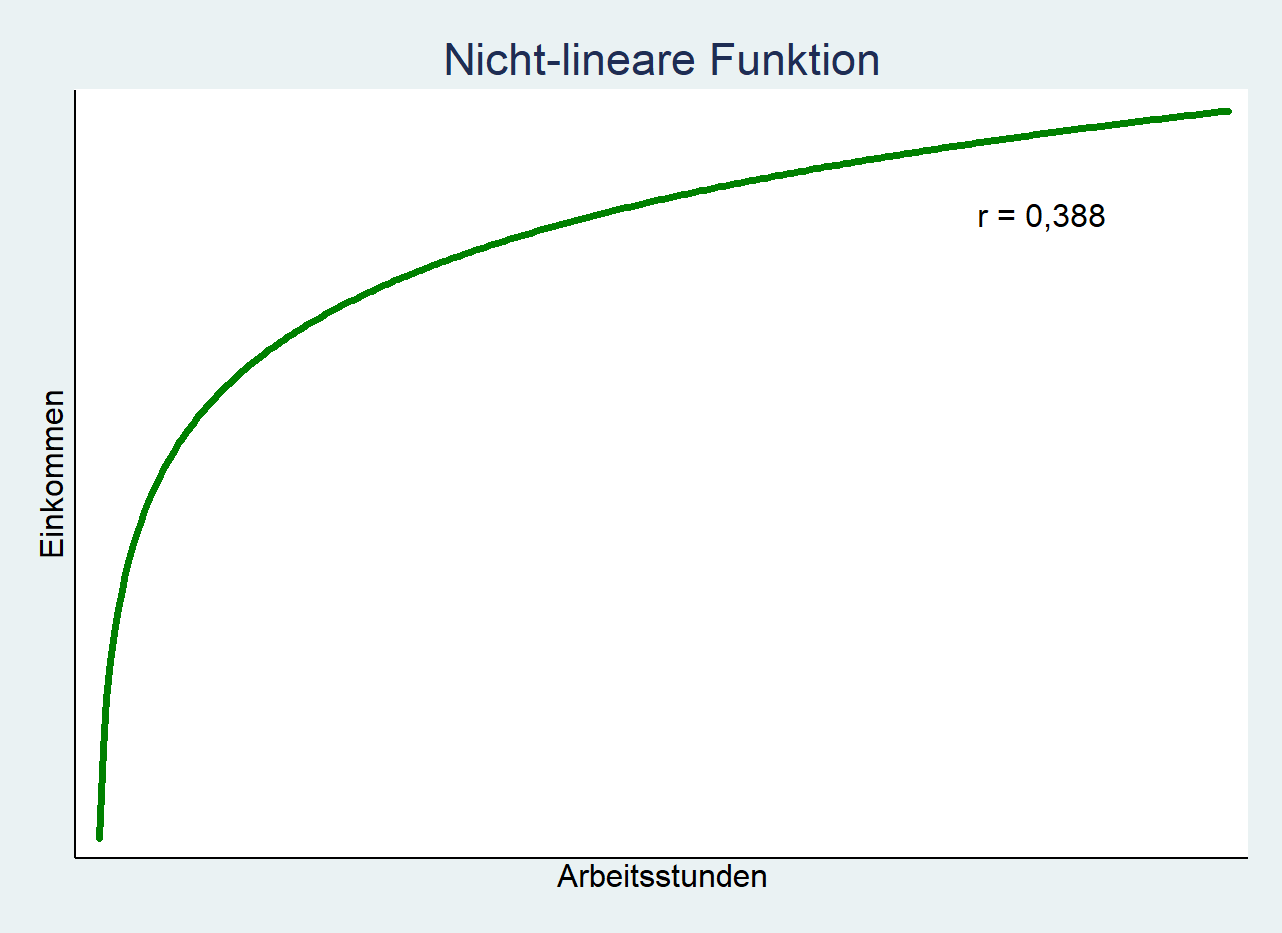
In der Grafik lässt sich deutlich sehen, dass der Zusammenhang der beiden Variablen kurvilinear ist. Mit steigendem \(x\) steigt \(y\) zu Beginn sehr schnell, mit zunehmenden \(x\) nimmt allerdings die Steigung von \(y\) ab. Monotonie liegt dagegen vor, da \(y\) immer steigt.
Nehmen wir zur Verdeutlichung ein Beispiel: Wir betrachten den Zusammenhang zwischen Einkommen (\(y\)) und Wochenarbeitszeit (\(x\)). In diesem Beispiel würde bei einer geringen Wochenstundenzahl das Einkommen stärker steigen (bei einer Erhöhung um eine Stunde), als es dies bei einer bereits hohen Wochenstundenzahl tun würde.
Die Punkte liegen recht eng zusammen, so dass der niedrige Wert des Korrelationskoeffizienten zusätzlich irreführend erscheint. Dies liegt an der Verletzung der Bedingung der Linearität.
Sollte der Zusammenhang zwischen zwei metrischen Variablen nicht linear sein, dann kann zur Berechnung der Korrelation Spearmans \(\rho\) genutzt werden (oder eine der Variable muss transformiert werden, so dass der Zusammenhang linear ist).