Gesetz der großen Zahlen
Zuerst führen wir in das Gesetz der großen Zahlen ein. Vereinfacht gesagt, besagt das Gesetz der großen Zahlen folgendes: „Je größer die Stichprobe (..), um so eher kann man eine ziemlich genaue Übereinstimmung zwischen Stichprobenwerten und Parametern der Grundgesamtheit erwarten“ (Kromrey et al., 2016, p. 279).
Als einfaches Beispiel zählt der Wurf eines sechsseitigen Würfels: Jede Augenzahl (Seite) hat bei jedem Wurf eine Wahrscheinlichkeit von \(\frac{1}{6}\) geworfen zu werden. Wiederholt man den Wurf immer wieder, stellt man fest, dass die Wahrscheinlichkeit der Augenzahl bei wiederholter Durchführung in Richtung der Eintrittswahrscheinlichkeit (\(\frac{1}{6}\)) tendiert. Dies wird auch als schwaches Gesetz der großen Zahl beschrieben. Das starke Gesetz der großen Zahl wird auf den Standardfehler angewendet. Der Standardfehler (dazu gleich mehr) tendiert gegen \(0\), je größer der Stichprobenumfang wird. Denn mit einem größerem Stichprobenumfang wird die Informationsunsicherheit geringer, die bei der Stichprobenziehung vorliegt.
Verdeutlichen Sie sich dazu das einfache Beispiel: Wenn die Stichprobe gleich der Grundgesamtheit ist, beträgt der Standardfehler der Stichprobenziehung \(0\), da in diesem Fall der Populationsmittelwert (\(\mu\)) dem Grundgesamtheitsmittelwert (\(\bar{x}\)) entspricht. Nichtsdestotrotz kann selbst bei großen Stichproben der Wert eines Merkmals von dem Wert in der Population abweichen, allerdings ist dies sehr unwahrscheinlich.
Stichprobenkennwert
Um Rückschlüsse auf eine jeweilige Population ziehen zu können, werden in der Regel Stichprobenkennwerte berechnet. Einer dieser Stichprobenkennwerte ist der Mittelwert. Zur Wiederholung hier noch einmal die Logik der Inferenz: Aus der Grundgesamtheit ziehen wir zufällig eine Stichprobe. In dieser Stichprobe ziehen wir Schlüsse über Stichprobenkennwerte, die wir dann auf die Grundgesamtheit beziehen können. Der letzte Schritt bezeichnet die Inferenz.
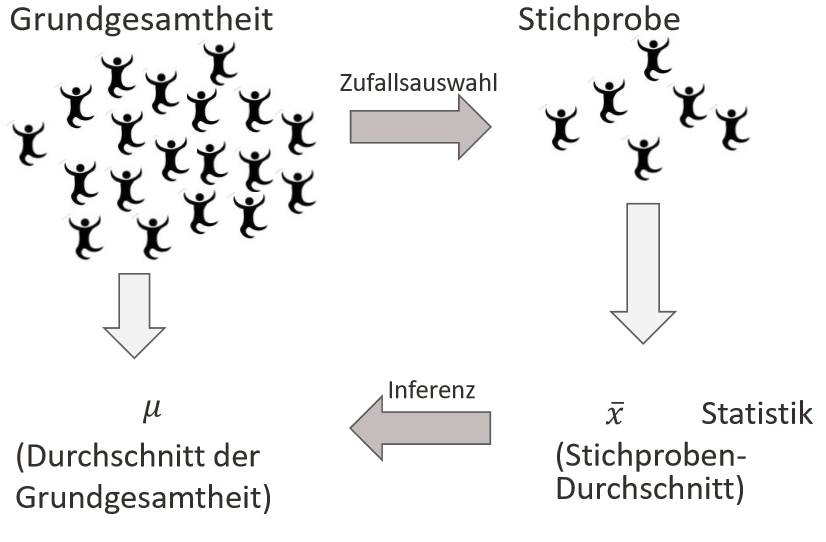
Das arithmetische Mittel \(\bar{x}\) der Zufallsstichprobe kann vom Durchschnittswert der Grundgesamtheit (auch Erwartungswert) abweichen. Warum? Stichprobendaten sind immer unvollständige Daten, denn es ist keine Vollerhebung. Diese Abweichung ist aber zufällig. Diese zufällige Abweichung wird als Stichprobenfehler (auch sampling error) bezeichnet.
Was bedeutet dies? Wenn wir zum Beispiel für eine Grundgesamtheit mehrere Zufallsstichproben durchführen, wird das arithmetische Mittel (\(\bar{x}\)) einer Variable zwischen den einzelnen Stichproben voneinander abweichen. Das arithmetische Mittel jeder einzelnen Stichprobe bezeichnet man als Stichprobenkennwert (hier Mittelwert). Da sich beim zufälligen Ziehen einer Stichprobe die Zusammensetzung der Beobachtungen unterscheiden wird, erhält jede Stichprobe einen unterschiedlichen Stichprobenkennwert (Mittelwert). In der Grafik sehen wir dargestellt, dass wir \(m\) Stichproben aus der Grundgesamtheit ziehen. Jede Stichprobe variiert zufällig, da diese zufällig aus der Grundgesamtheit gezogen wird. Für jede Stichprobe ergibt sich daher ein verschiedener Stichprobenkennwert (Mittelwert).
Man erhält dann zum Beispiel für das arithmetische Mittel des Alters (\(\bar{x}_{Alter}\)) bei hier nun vier dargestellten Stichproben folgende Werte als Stichprobenkennwert (Mittelwert):
| Var | Stichprobe 1 | Stichprobe 2 | Stichprobe 3 | Stichprobe 4 |
|---|---|---|---|---|
| \(\bar{x} _{Alter}\) | \(45.6\) | \(39.7\) | \(43.3\) | \(49.4\) |
Diese unterschiedlichen Stichprobenkennwerte bilden dann die Verteilung einer Stichprobenstatistik über die gesamten Stichproben, auch Stichprobenverteilung / Stichprobenkennwerteverteilung (auch sampling distribution) benannt, aus der sich der Stichprobenfehler berechnen lässt. Diese Schwankung des arithmetischen Mittels über verschiedene Stichproben misst man mit dem Stichprobenfehler.