t-Verteilung
Eine weitere wichtige Verteilungsform neben Normal- und Standardnormalverteilung ist die t-Verteilung.
Die t-Verteilung ist glockenförmig, aber flacher als die Normalverteilung. Sie wird insbesondere dann genutzt, wenn weniger als 30 Stichproben herangezogen werden oder wir die Varianz (\(\sigma^2\)) nicht kennen. Dies wird insbesondere bei einigen Hypothesentests in der Statistik angewendet. Des Weiteren geht die t-Verteilung bei großen Fallzahlen in eine Normalverteilung über.
Die t-Verteilung geht zurück auf William S. Gosset und stellt eine „genauere“ z-Verteilung dar. Ein Problem der Standardnormalverteilung liegt darin, dass mehr Annahmen getroffen werden, als in sozialwissenschaftlichen Forschungssituationen oftmals vorhanden sind. So ist die Standardabweichung zur Berechnung des Standardfehlers für die Grundgesamtheit meist nicht bekannt. Die „wahre Streuung“ wird daher aus der Stichprobenstreuung geschätzt, was zu Unsicherheit führt. Bei großen Stichproben ist dies unproblematisch, bei kleineren jedoch birgt dies Probleme. Daher wird bei kleineren Stichproben die t-Verteilung angenommen.
Die Form der t-Verteilung hängt dabei von der Anzahl der Freiheitsgrade (df = degrees of freedom) ab, die wiederum die Stichprobengröße widerspiegelt. Die Freiheitsgerade berechnen sich aus der Stichprobengröße: \(df=n - 1\). Je höher die Anzahl der Freiheitsgrade, desto besser repräsentiert die Stichprobenvarianz die Populationsvarianz und desto besser repräsentiert die \(t\)-Statistik den entsprechenden \(z\)-Wert.
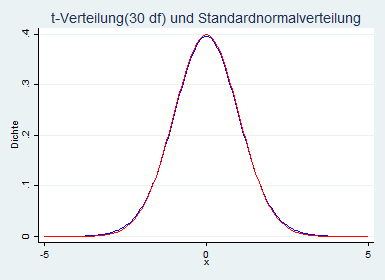
Die erste der untenstehenden Grafiken zeigt eine t-Verteilung, bei der sich die Anzahl der Freiheitsgrade verändert. In der zweiten Grafik können Sie sehen, dass die t-Verteilung bereits ab 30 Freiheitsgraden bereits nahezu identisch mit der Standardnormalverteilung ist. Optisch ist kein Unterschied mehr erkennbar.
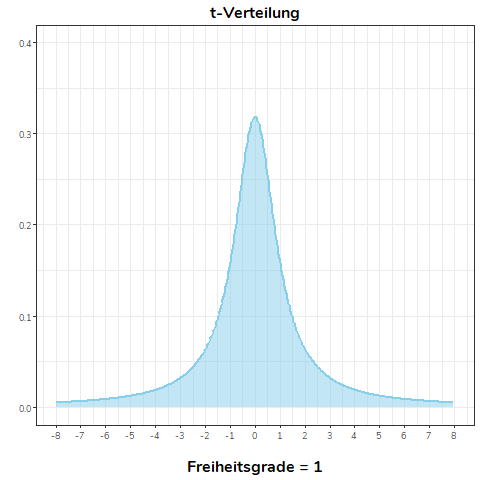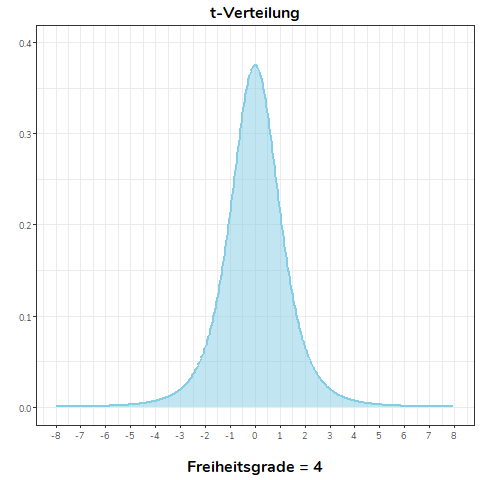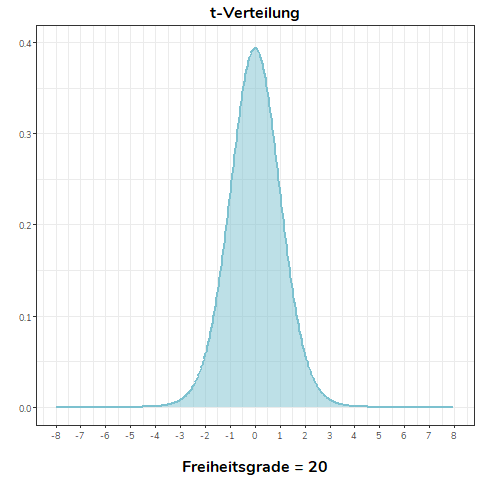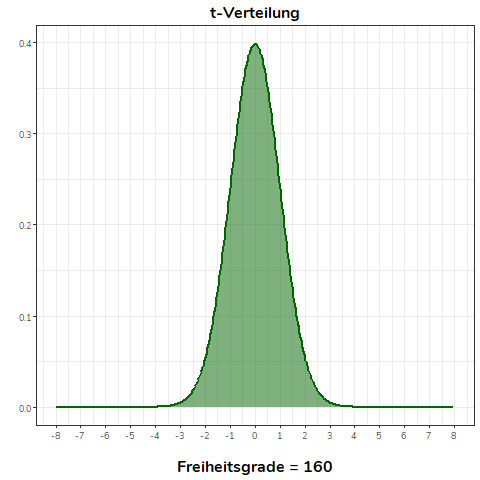
Siehe auch: Bortz & Schuster (2010, Kapitel 5.5.2)