Diskrete Zufallsvariable
Für diskrete Zufallsvariablen wird die Verteilungsfunktion aus der Wahrscheinlichkeitsfunktion, die jedem \(x_i\) genau eine Wahrscheinlichkeit \(P(X= x_i)\) zuordnet, berechnet. Dabei wird eine kumulative Wahrscheinlichkeit \(P(X\leq x_i)\) gebildet. Wichtig hierbei ist, dass die Verteilungsfunktion \(F(x)\) monoton und rechtsseitig steigend ist. Ebenso gilt, dass diese Funktion Werte zwischen \(0\) und \(1\) annimmt (\(F(x) \in (0,1)\)). Die Grenzwerte werden daher wie folgt beschrieben \(lim_{x \rightarrow - \infty} F(x) = 0\) und \(lim_{x \rightarrow -\infty}F(x) = 1\). Die Darstellung der Verteilungsfunktion ist eine Treppenfunktion: An den entsprechenden Datenpunkten macht die Funktion jeweils einen Sprung.
Wir nehmen dazu folgendes Beispiel an: Wir werfen einen 6-seitigen Würfel zweimal und addieren die Werte zur Augensumme. DIe Zufallsvariable \(X\) umfasst die Augensumme, die Werte von \(2\) bis \(12\) annehmen kann (\(X \in (2,12)\). Pro Würfelwurf gilt für jede der 6 Seiten eine Wahrscheinlichkeit von \(\frac {1}{6}\). Im Beispiel liegt eine diskrete Gleichverteilung vor: Diese ist dadurch charakterisiert, dass verschiede Werte \(x_1, x_2, ..., x_k\) mit gleicher Wahrscheinlichkeit angenommen werden.
Jetzt teilen wir dem Zufallsexperiment reelle Zahlen zu (\(\omega \rightarrow x\)). Wir erhalten im Zufallsexperiments \(\Omega\) folgende Werte \(\omega_i\) (die zwei Würfe, 11 für 1 bei erstem und zweitem Wurf) und die Zuordnung der Augensumme \(x_i\) (hier nur die Auswahl für Würfe, in denen eine 1 vorkommt).

Wenn wir also zuerst eine \(1\) und dann eine \(4\) würfeln (5. Spalte), erhalten wir als Ergebnis der Augensumme \(5\). Für ein Würfelergebnis von zuerst \(6\) und dann \(1\) erhalten wir \(7\).
Wir können diese Ergebnisse auch zusammenfassen. \[X(\omega) = \begin{cases} 2 & \text{für } \omega = 11 \\ 3 & \text{für } \omega = 12, 21 \\ 4 & \text{für } \omega = 13, 31, 22 \\ 5 & \text{für } \omega = 14, 41, 23, 32 \\ 6 & \text{für } \omega = 15, 51, 24, 42, 33 \\ 7 & \text{für } \omega = 16, 61, 25, 52, 34, 43 \\ 8 & \text{für } \omega = 26, 62, 35, 53, 44 \\ 9 & \text{für } \omega = 36, 63, 45, 54 \\ 10 & \text{für } \omega = 46, 64, 55 \\ 11 & \text{für } \omega = 56, 65 \\ 12 & \text{für } \omega = 66 \end{cases}\]
Der Wert 9 wird zugeordnet, wenn folgende Würfelpaare auftreten: \(3\) & \(6\), \(6\) &\(3\), \(4\) & \(5\), \(5\) & \(4\).
Nun berechnen wir die Wahrscheinlichkeitsfunktion (\(x \rightarrow P(X = x)\)): Jeder Augensumme \(x\) ordnet wir die Wahrscheinlichkeit zu. Insgesamt können \(36\) Ereignisse in der Zufallsvariable auftreten (\(|\Omega| = 36\). Beachte: \(\omega = 16\) ist ein anderes Ereignis als \(\omega = 61\), auch wenn die Augensumme gleich ist. Im ersten Fall wird zuerst die \(1\) und dann die \(6\) gewürfelt, im zweiten Fall erst die \(6\) und dann die \(1\).
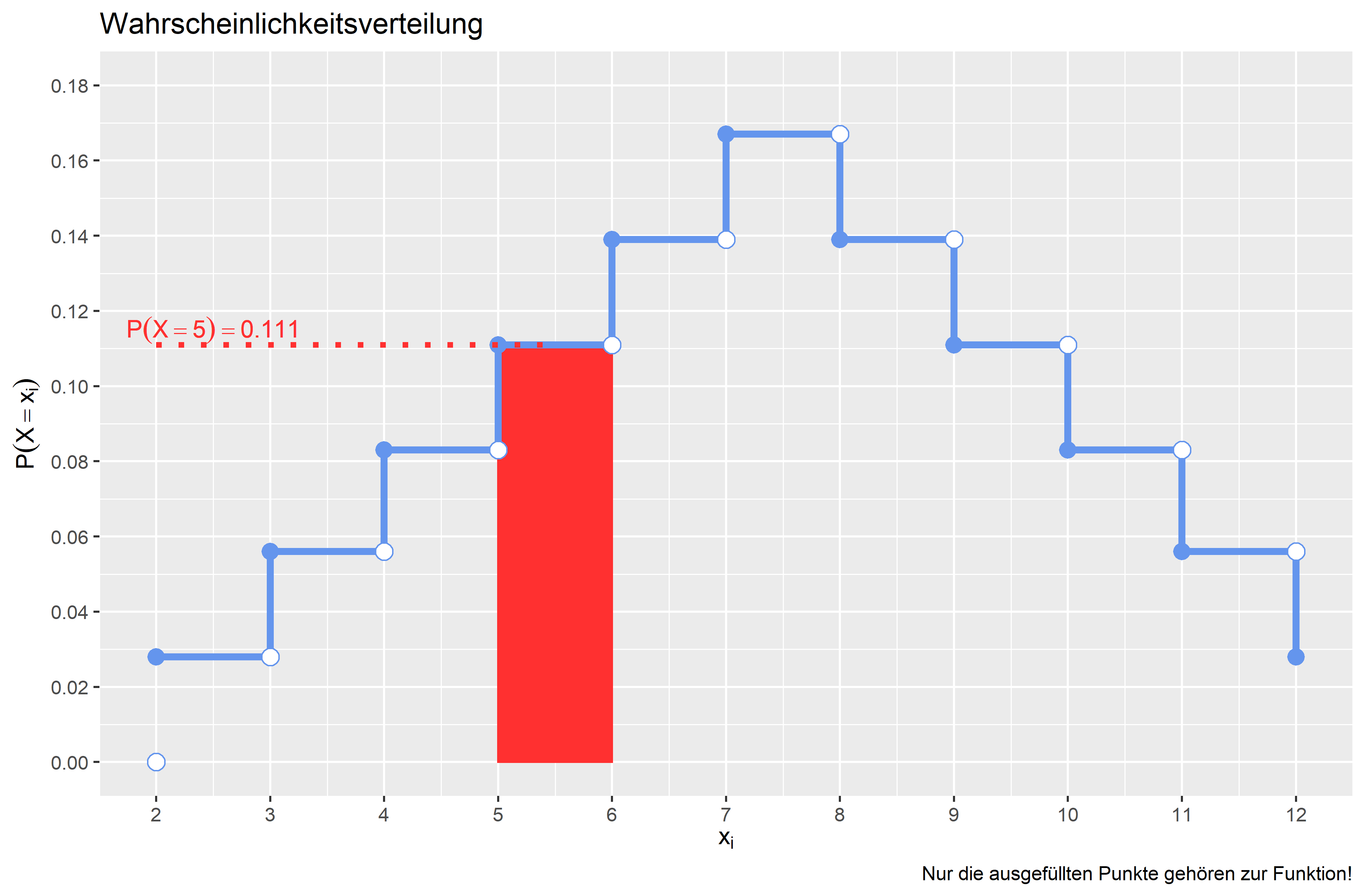
Wir möchten nun die Wahrscheinlichkeit errechnen, dass \(X = 5\) ist. Zuerst können wir den Erwartungswert festlegen. Wir zählen also wie oft, dieses Ereignis eintreten kann: \(E(X = 5) = {14, 41, 23, 32} \Rightarrow |E| = 4\).
Das Ereignis kann in \(4\) Situtationen eintreten: Wenn zuerst eine \(1\) und dann eine \(4\) gewürfelt wird, wenn zuerst eine \(4\) und dann eine \(1\) gewürfelt wird, wenn zuerst eine \(2\) und dann eine \(3\) gewürfelt wird und wenn zuerst eine \(3\) und dann eine \(2\) gewürfelt wird.
Die Wahrscheinlichkeit, dass \(X=5\) ist, berechnet sich wie folgt: \(P(X = 5) = \frac {|E|}{|\Omega|} = \frac {4}{36} = \frac{1}{9} \approx 0,111\) Die Wahrscheinlichkeit, dass wir in unserem Zufallsexperiment die Augenzahl 5 werfen, liegt also bei \(0,111 (11 \%)\).
Berechnen wir eine weitere Wahrscheinlichkeit, diesmal dafür, dass die Augenzahl gleich \(11\) ist: \(E(X=11)={56, 65} \Rightarrow |E| = 2\) \(P(X=11) = \frac {|E|}{|\Omega|} = \frac {2}{36} = \frac{1}{18} \approx 0,056\) Die Wahrscheinlichkeit, dass wir in unserem Zufallsexperiment die Augenzahl 11 werfen, liegt also bei \(0,056 (5,6\%)\).
Hier können Sie die Tabelle mit den zugeordneten Wahrscheinlichkeitswerte für jede Summe der Augenzahl sehen:

In den Grafiken sehen Sie verschiedene Bereiche der Verteilungsfunktion markiert, die weiter unten auch berechnet werden. Beachten Sie: Auch wenn hier eine Fläche markiert ist, ist bei diskreten Variablen die Fläche nicht gleich der Wahrscheinlichkeit. Denn die Verteilungsfunktion ist kumulativ. D.h. dass der “Balken” der nächsthöheren Augenzahl schon die Wahrscheinlichkeit der vorherigen Augensummen inkludiert. Daher entspricht die Fläche eines Bereichs nicht der Wahrscheinlichkeit.
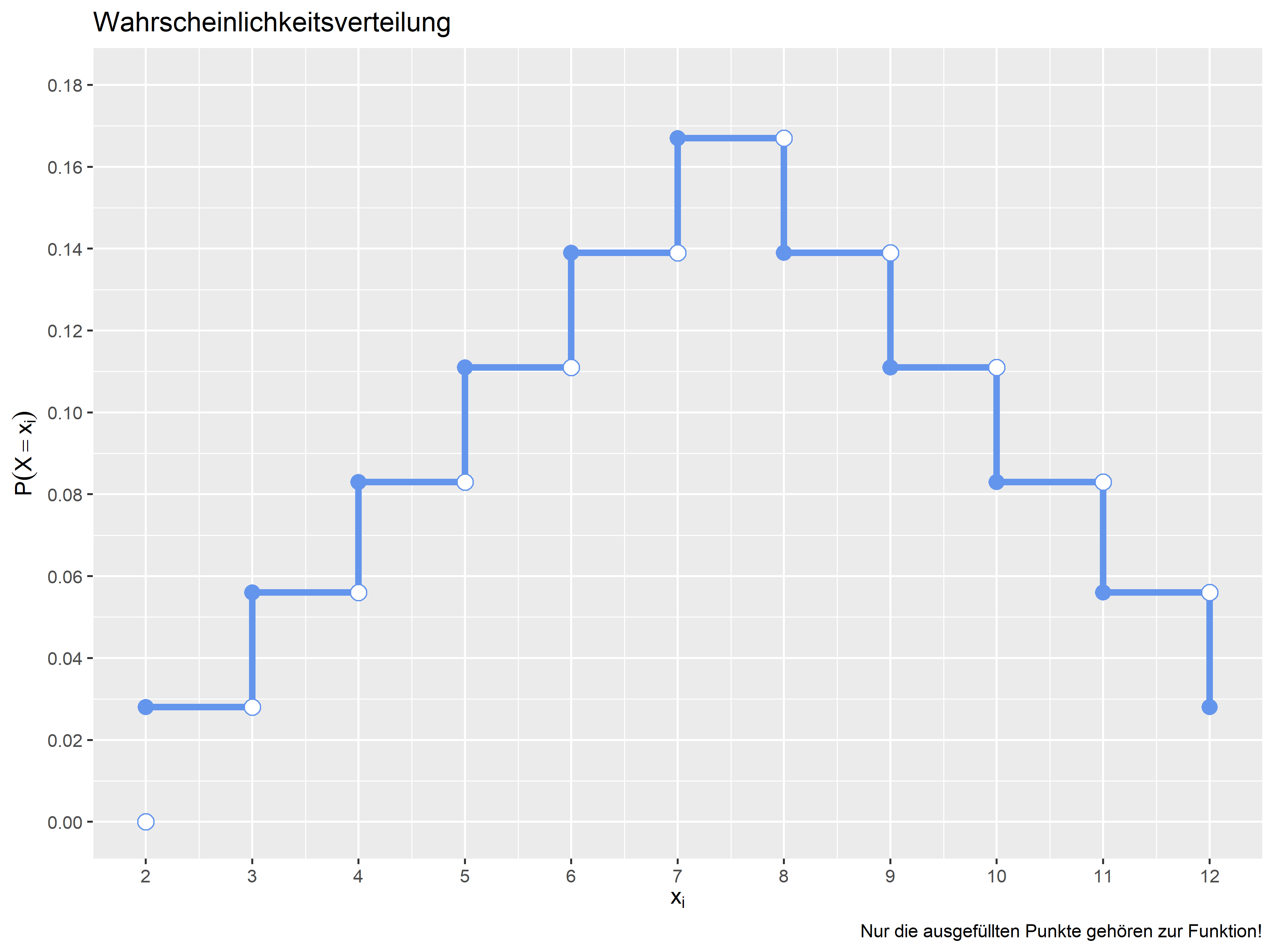
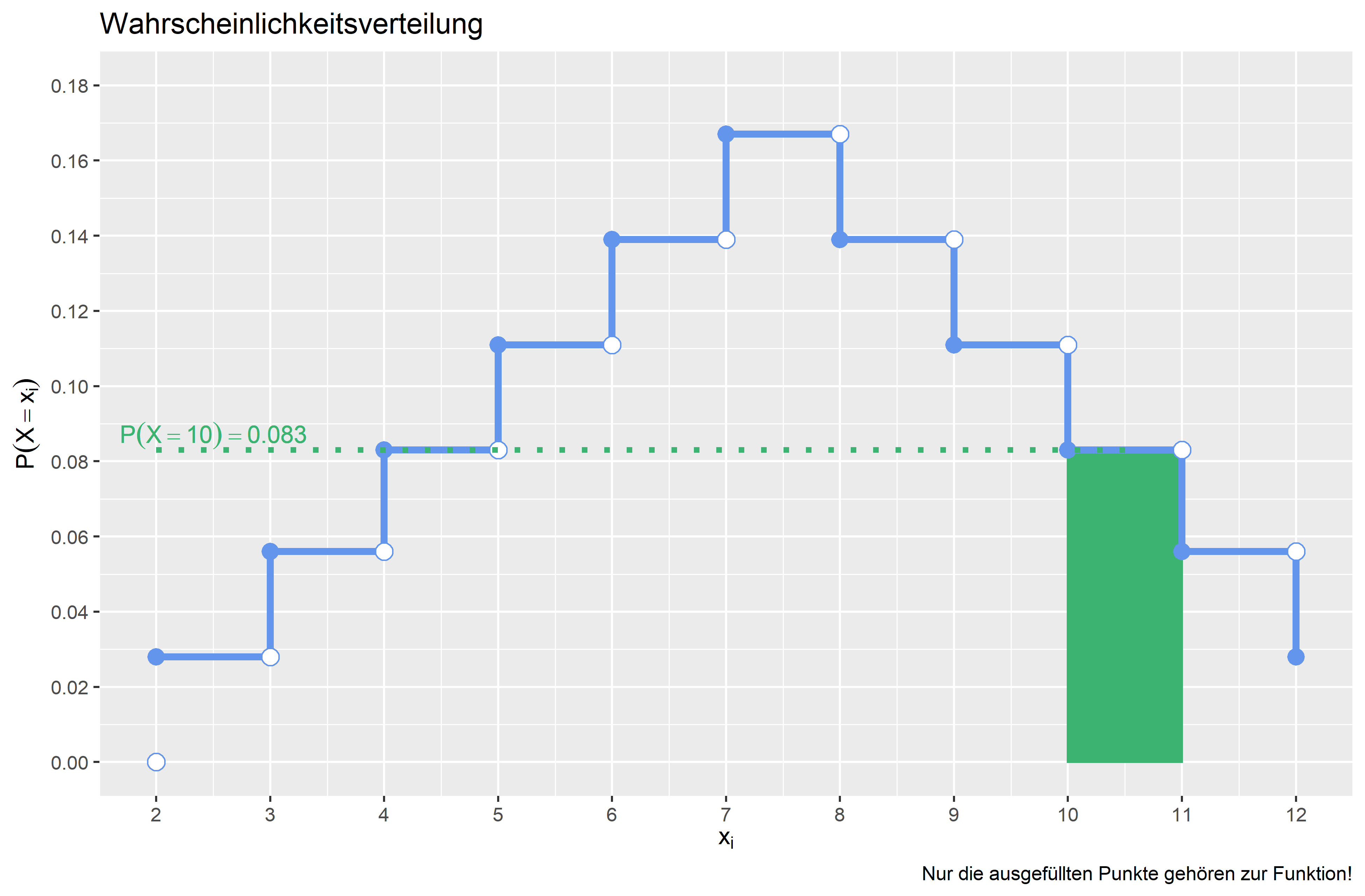
Der Tabelle kann man auch entnehmen, dass sich die Wahrscheinlichkeiten aufsummieren zu \(1\) (\(\sum_{i = 1}^n f(x_i)\)). Wir können auch hier zusammenfassend die Wahrscheinlichkeiten darstellen: \[f(x_i) = P(X=x_i) = \begin{cases} 0,028 & \text{für } x = 2 \\ 0,056 & \text{für } x = 3 \\ 0,083 & \text{für } x= 4\\ 0,111 & \text{für } x= 5 \\ 0,139 & \text{für } x = 6 \\ 0,167 & \text{für } x = 7 \\ 0,139 & \text{für } x= 8\\ 0,111 & \text{für } x= 9\\ 0,083 & \text{für } x= 10\\ 0,056 & \text{für } x= 11 \\ 0,028& \text{für } x= 12\end{cases}\]
Aus diesen errechneten Einzel-Wahrscheinlichkeiten können wir nun die Verteilungsfunktion bilden (\(x \rightarrow P(X \leq x)\)). Diese ordnet jeder Augensumme \(x\) die kumulierte Wahrscheinlichkeit zu: \(F(x) = P(X \leq x) = \sum_{x_i \leq x} P(X = x_i)\). Die Wahrscheinlichkeit, dass die Zufallsgröße \(X\) kleiner gleich \(x\) ist, ist also die Summe aller Einzelwahrscheinlichkeiten \(x_i\), solagen \(x_i \leq x\) gilt.
Berechnen wir ein Beispiel: Wir wollen \(X \leq 6\) berechnen. \(P(X \leq 6) = P(X=2) + P(X =3) + P(X=4) +P(X=5) + P(X=6) = \frac{1}{36} + \frac{2}{36} + \frac{3}{36} + \frac{4}{36} + \frac{5}{36} = \frac{15}{36} \approx 0.417\) Die Wahrscheinlichkeit höchstens eine Augensumme von \(6\) zu würfeln beträgt \(0,417 (41,7 \%)\).
Berechnen wir ein weiteres Beispiel: \(X \leq 3\) \(P(X \leq 3) = P(X = 2) + P(X=3) = \frac{1}{36} + \frac{2}{36} = \frac{3}{36} \approx 0.083\) Die Wahrscheinlichkeit höchstens eine Augensumme von \(3\) zu würfeln beträgt \(0.083 (8.3 \%)\).
Auch dieses können wir wieder in einer Tabelle für alle Werte darstellen:

Wie wir in der Tabelle sehen und auch schon weiter oben festgestellt haben, ist die Summe der Verteilungsfunktion \(1\).
Wir haben nun bereits errechnet, wie Wahrscheinlichkeiten bis zu einem bestimmten \(x_i\) berechnet werden. Doch wie berechnen wir die Wahrscheinlichkeit von \(P(X > x_i)\)? Oder die Wahrscheinlichkeit von Bereichen wie \(P(x_i < X \leq x_i+2)\)?
Für die Berechnung der Wahrscheinlichkeiten gelten folgende Regeln:
\(P(X \leq a) = F(a)\)
\(P(X < a) = F(a) - P(X =a)\)
\(P(X > a) = 1- F(a)\)
\(P(X \geq a) = 1-F(a) +P(X=a)\)
\(P(a < X \leq b) = F(b) - F(a)\)
\(P(a \leq X \leq b) = F(b) - F(a) + P(X =a)\)
\(P(a < X < b) = F(b)- F(a) -P(X=b)\)
\(P(a \leq X < b) = F(b)-F(a) + P(X=a) - P(X=b)\)
Machen wir nun ein paar Beispiele:
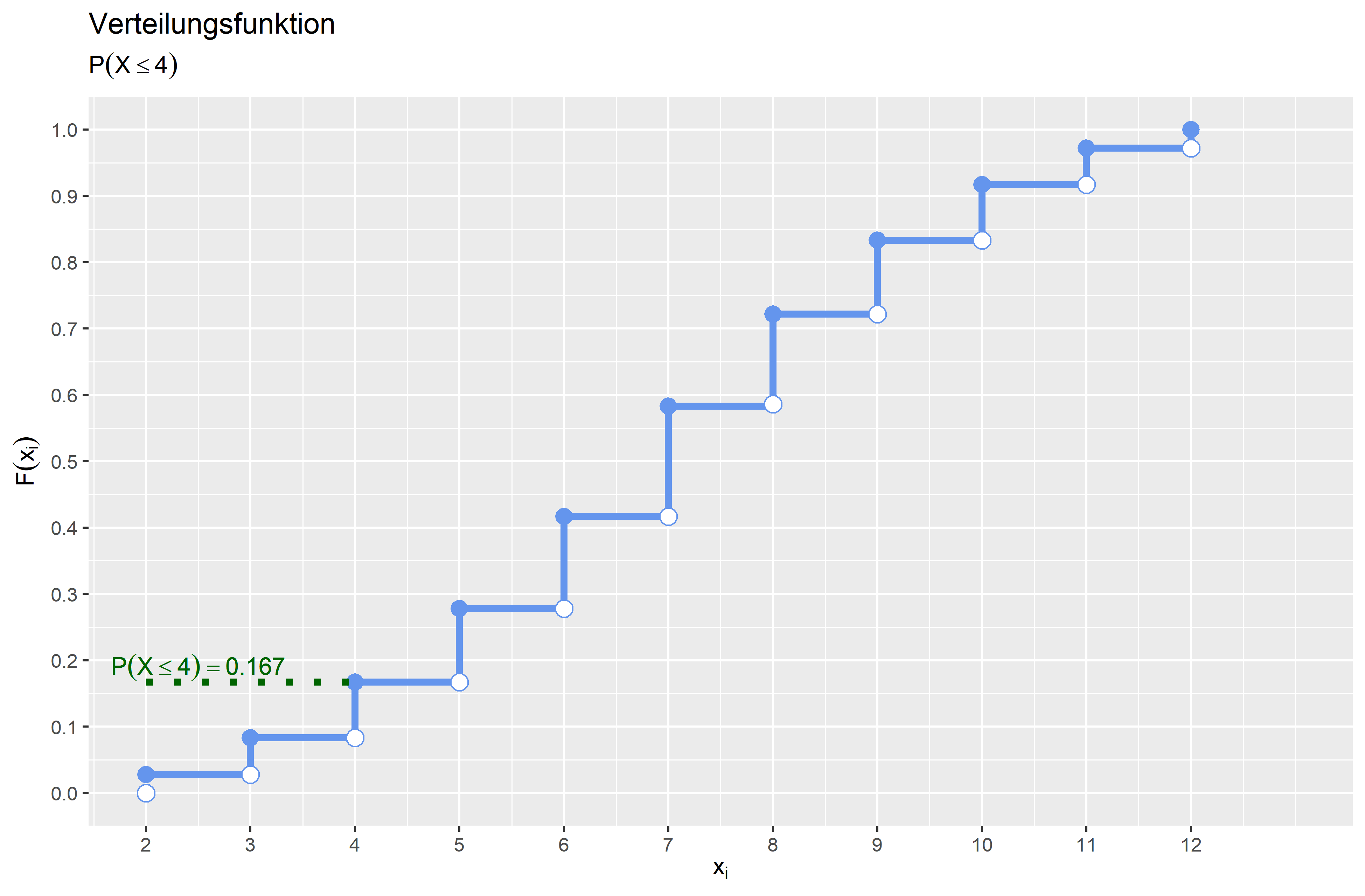
Siehe oben
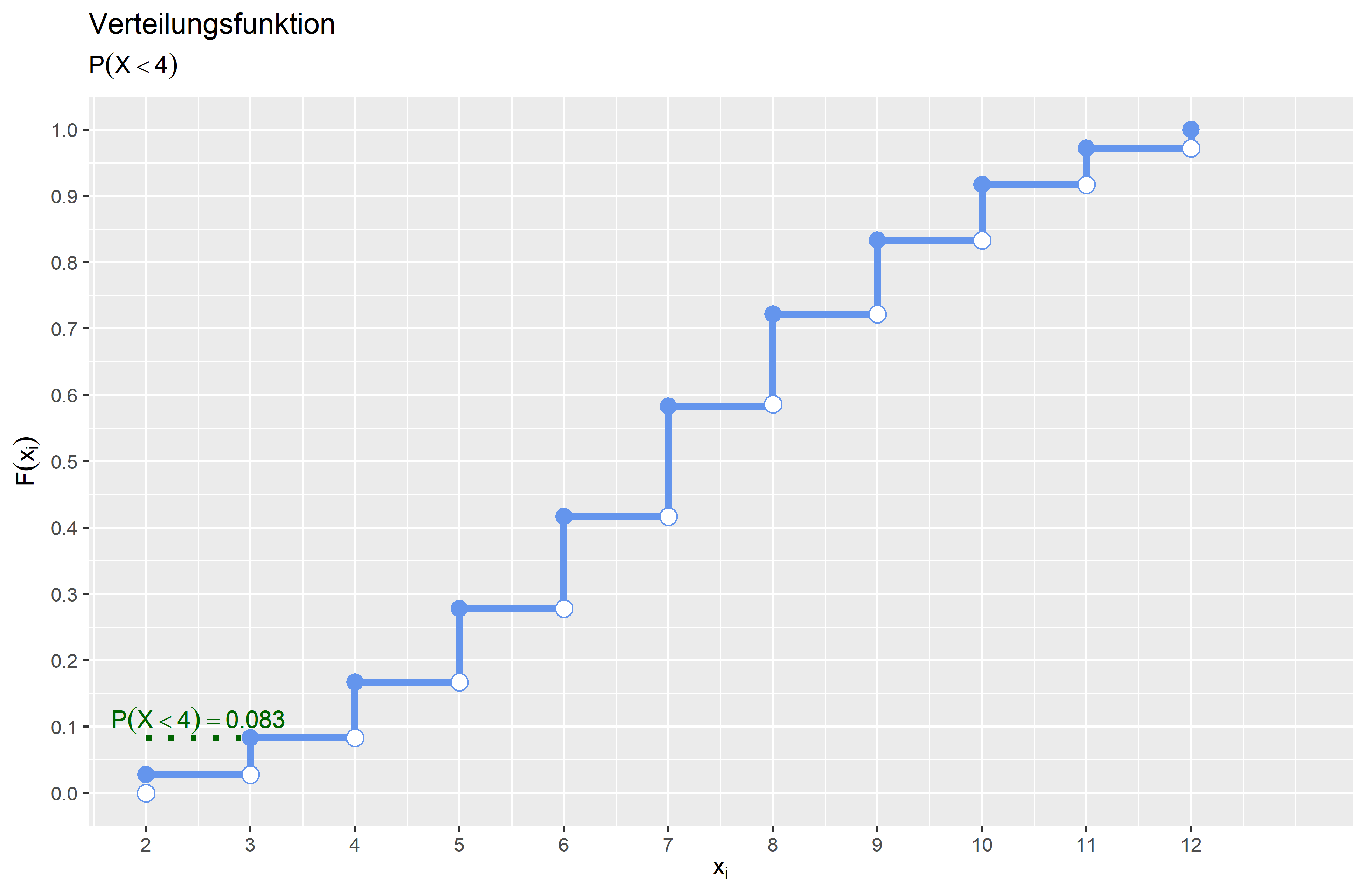
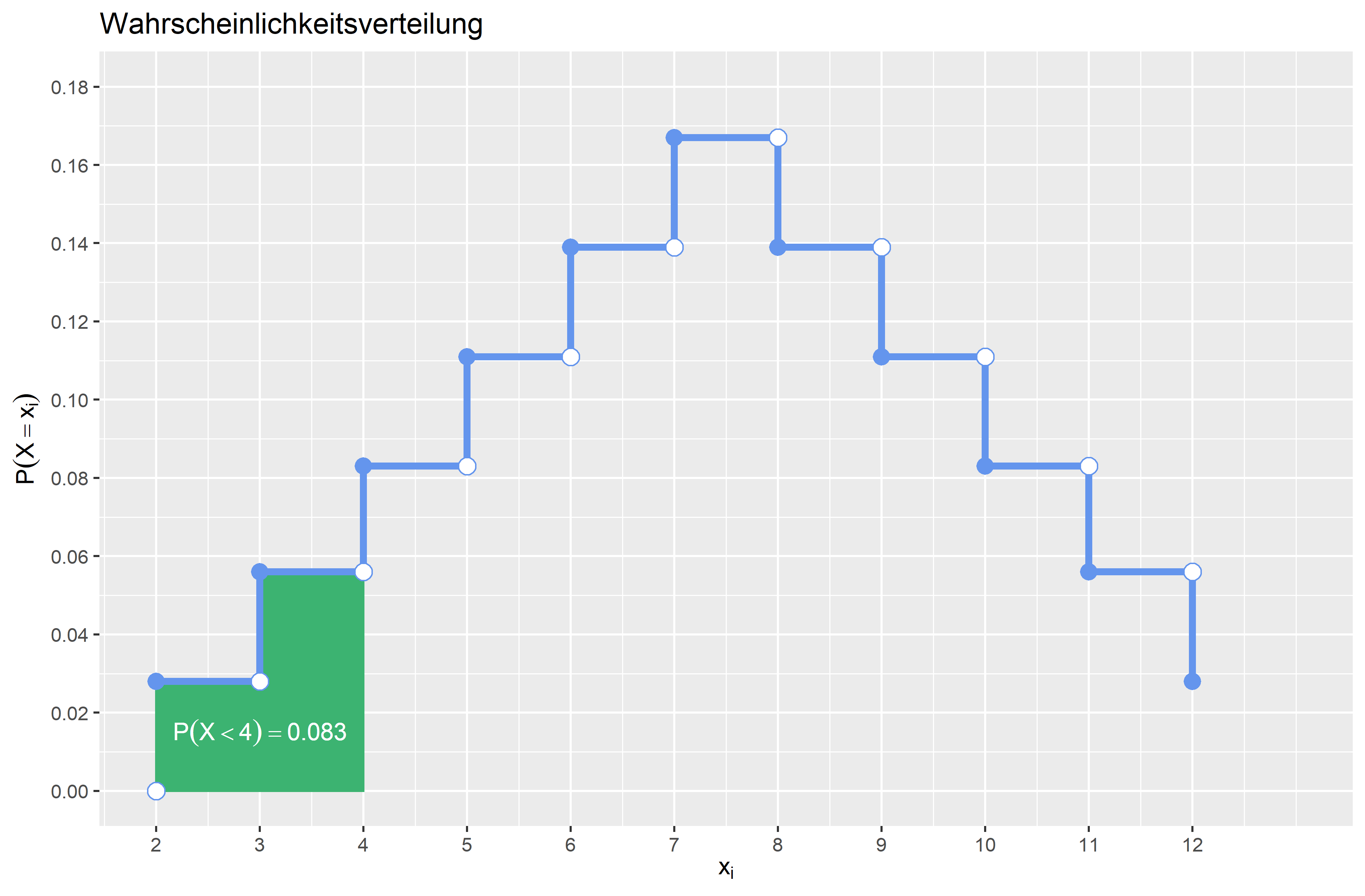
\(P(X < 4)\) \(P(X < 4) = F(4) - P(X=4) = \frac{6}{36} - \frac{3}{36} = \frac{3}{36} \approx 0.083\) Die Wahrscheinlichkeit, dass die Augensumme kleiner \(4\) ist, beträgt \(0.083 (8.3 \%)\).
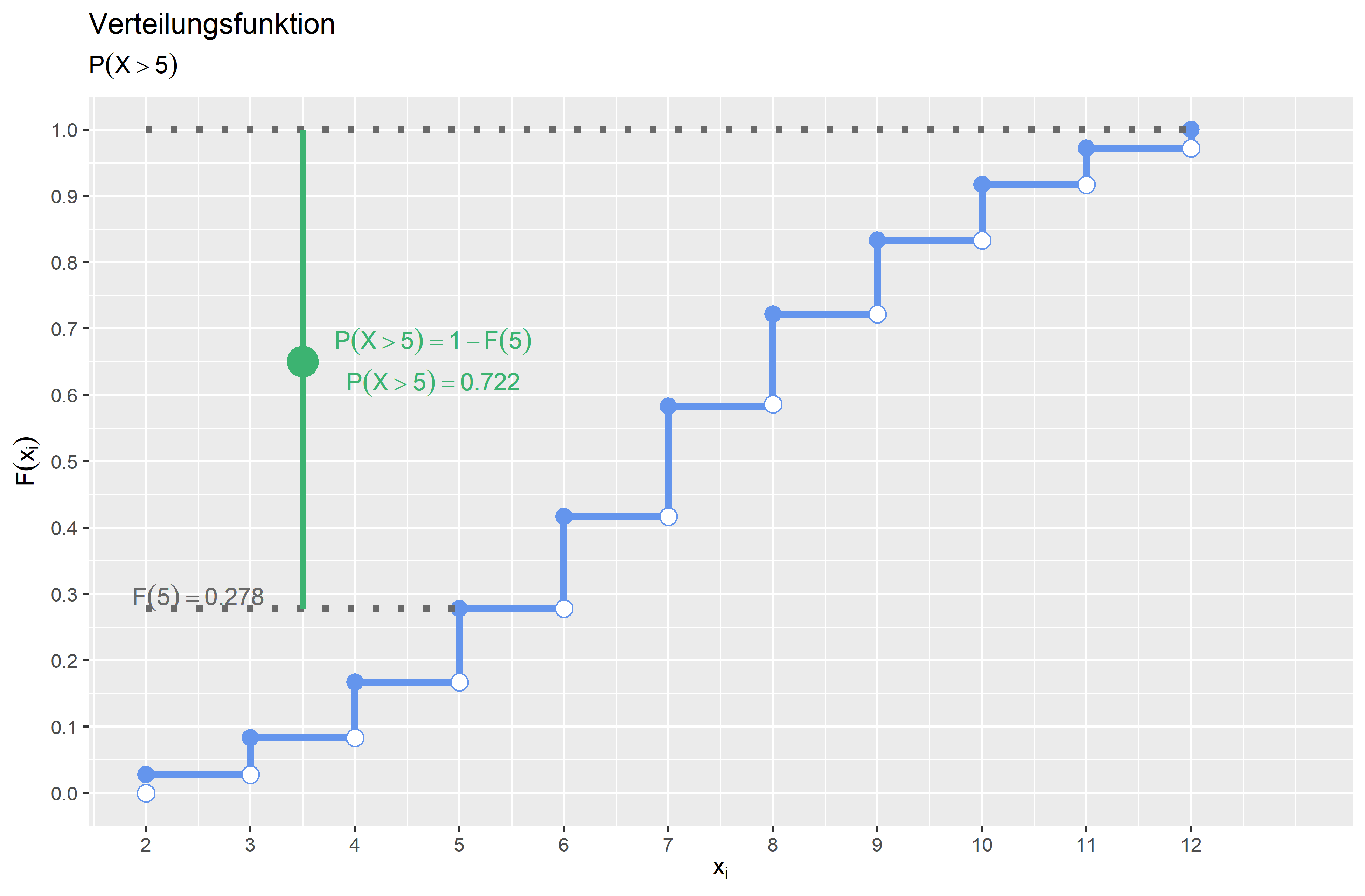
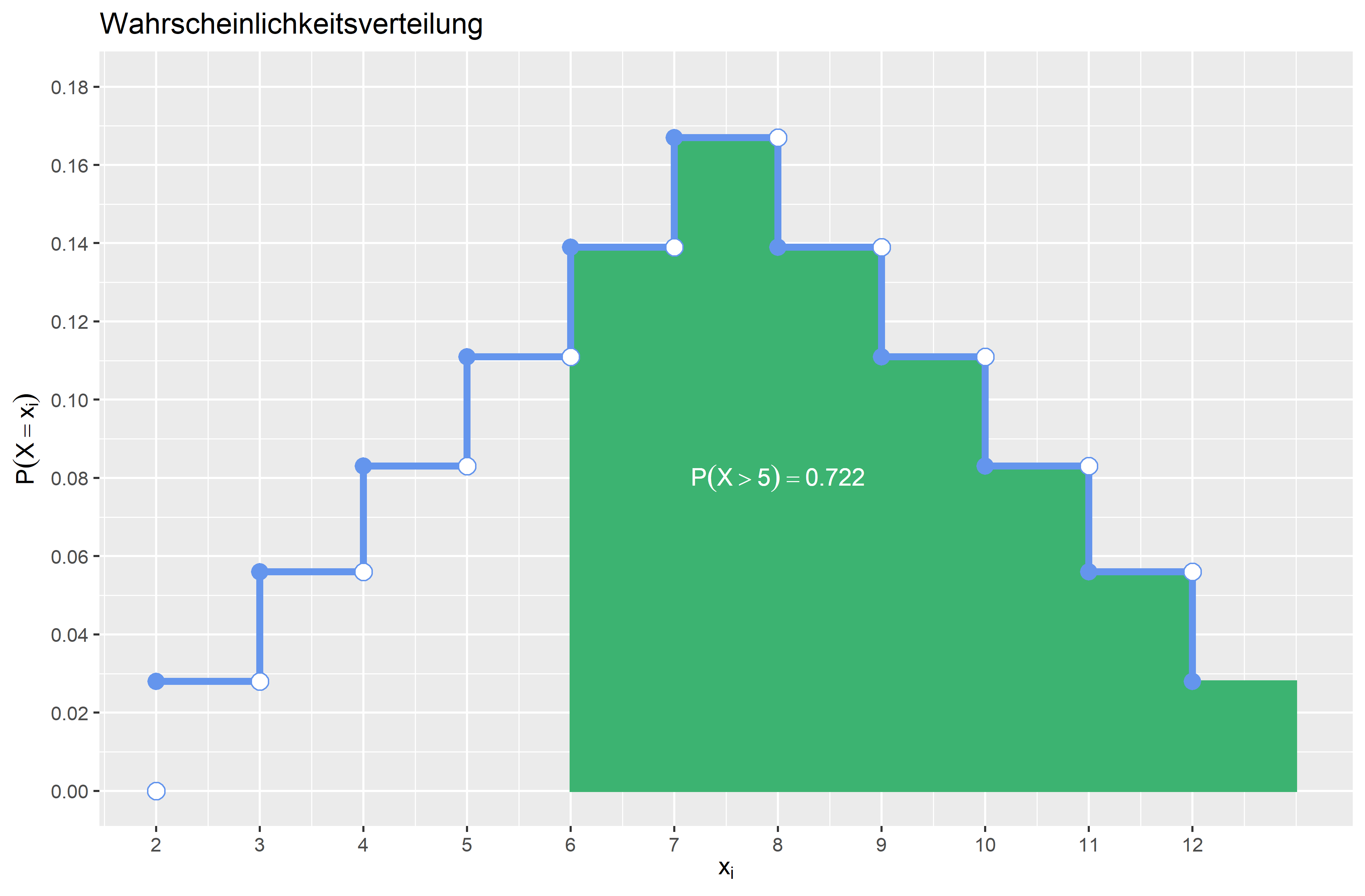
\(P(X > 5)\) \(P(X>5) = 1 - F(5) = 1- \frac{10}{36} = \frac{26}{36} \approx 0.722\) Die Wahrscheinlichkeit, dass die Augensumme größer als \(5\) ist liegt bei \(0.722 (72.2\%)\).
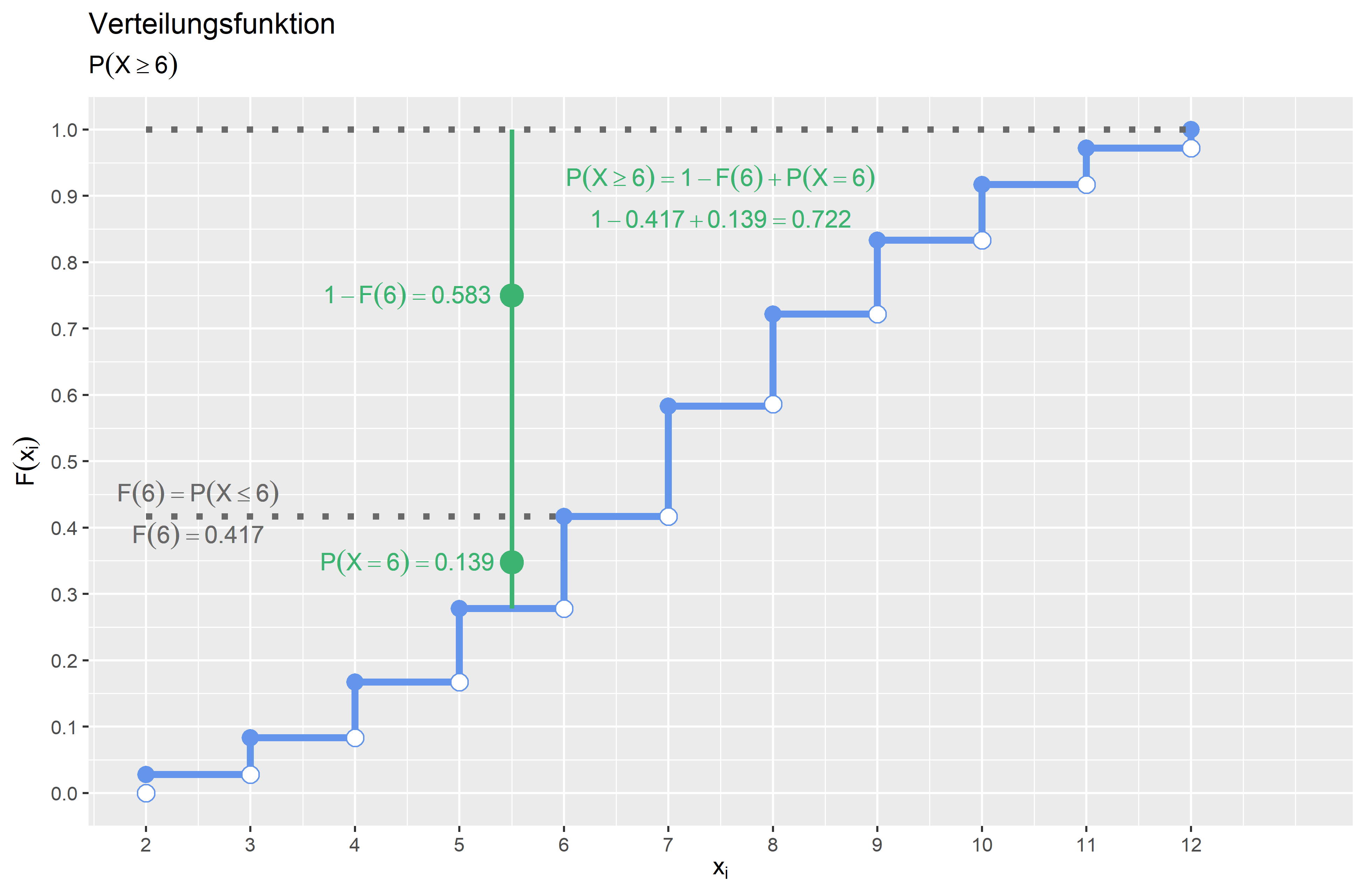
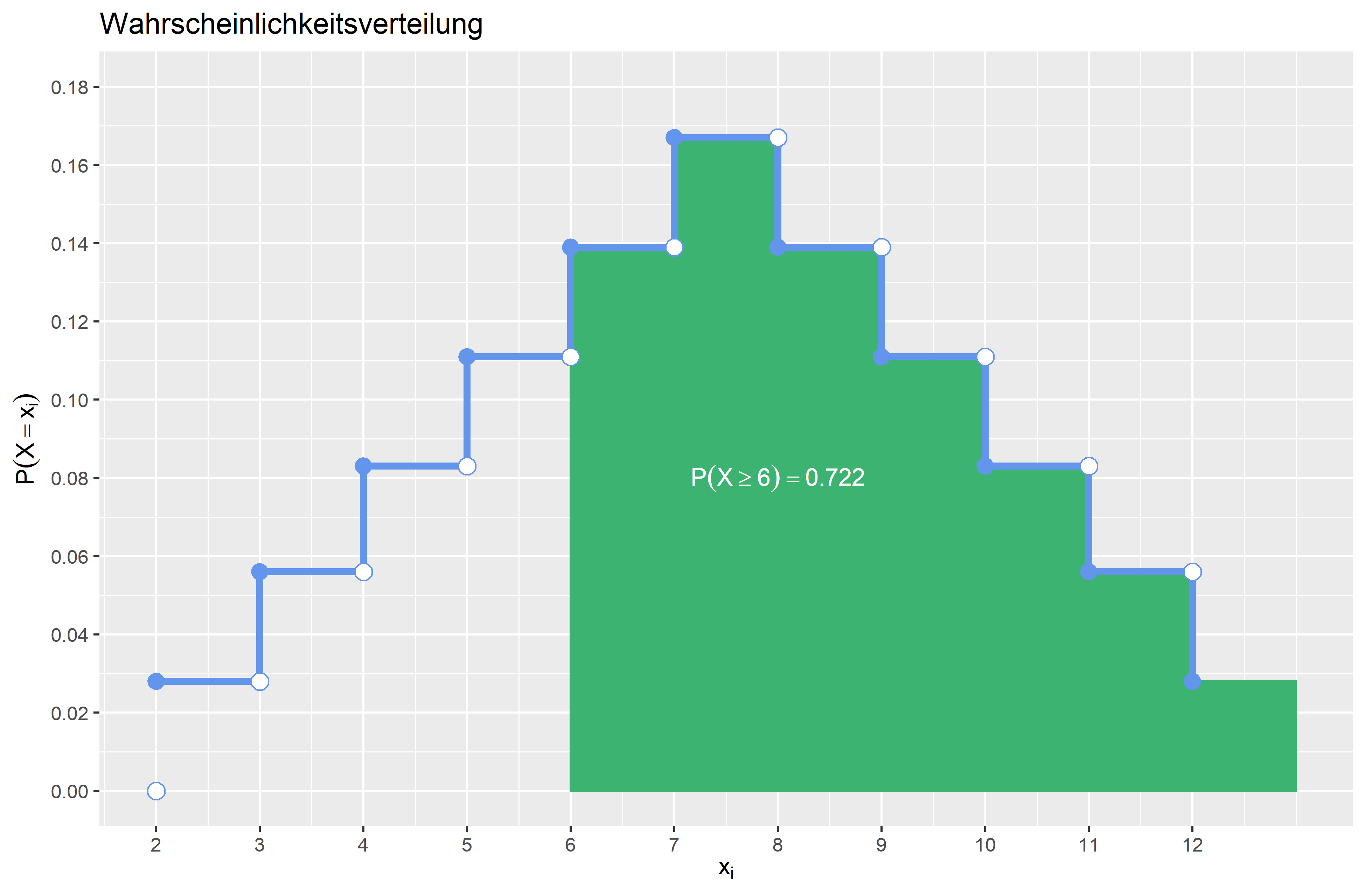
\(P(X \geq 6)\) \(P(X \geq 6) = 1-F(6) +P(X=6)= 1- \frac{15}{36} + \frac{5}{36} = \frac{26}{36} \approx 0.722\) Die Wahrscheinlichkeit, dass die Augensumme größer gleich \(6\) ist liegt bei \(0.722 (72.2\%)\).
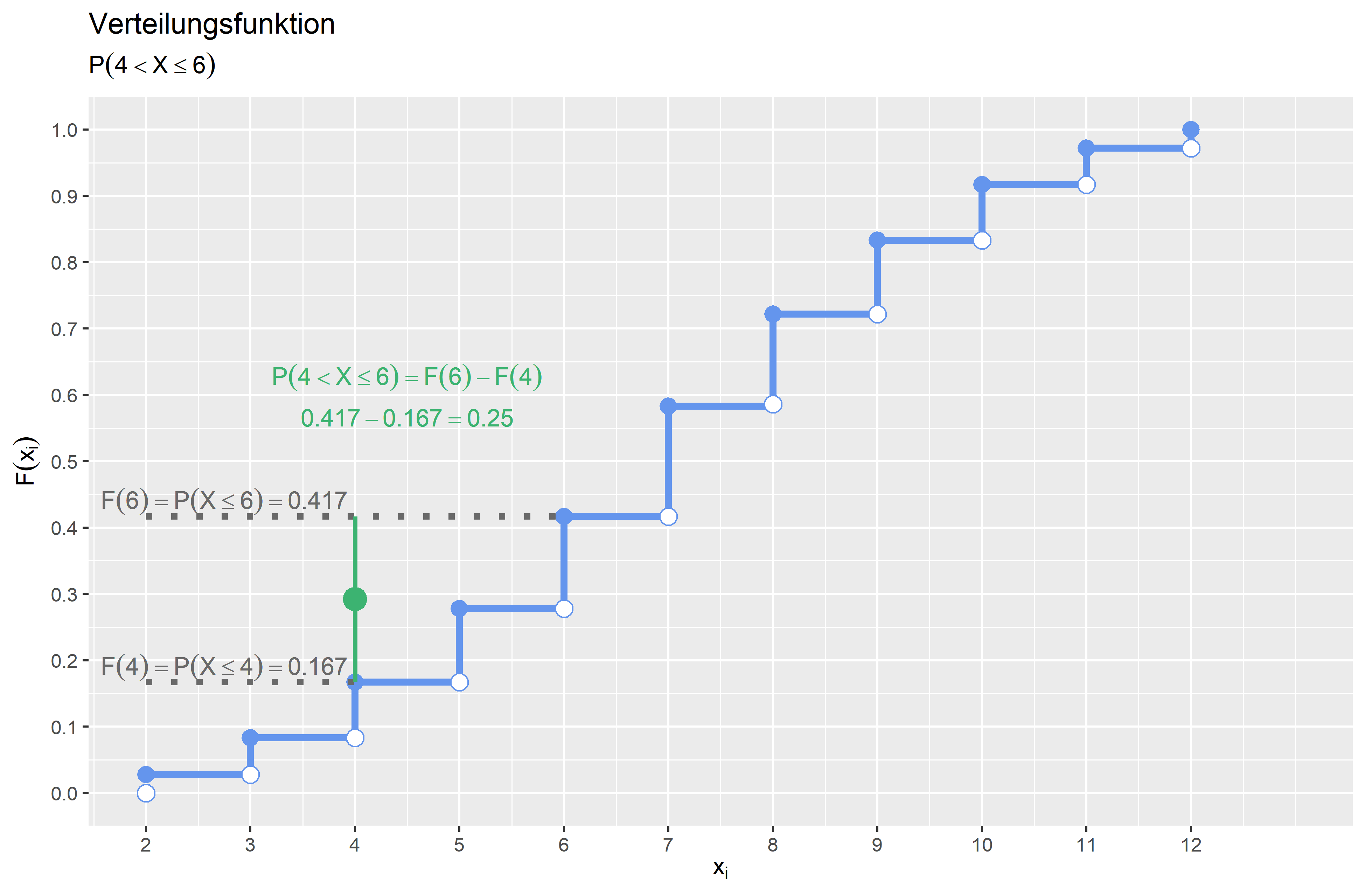
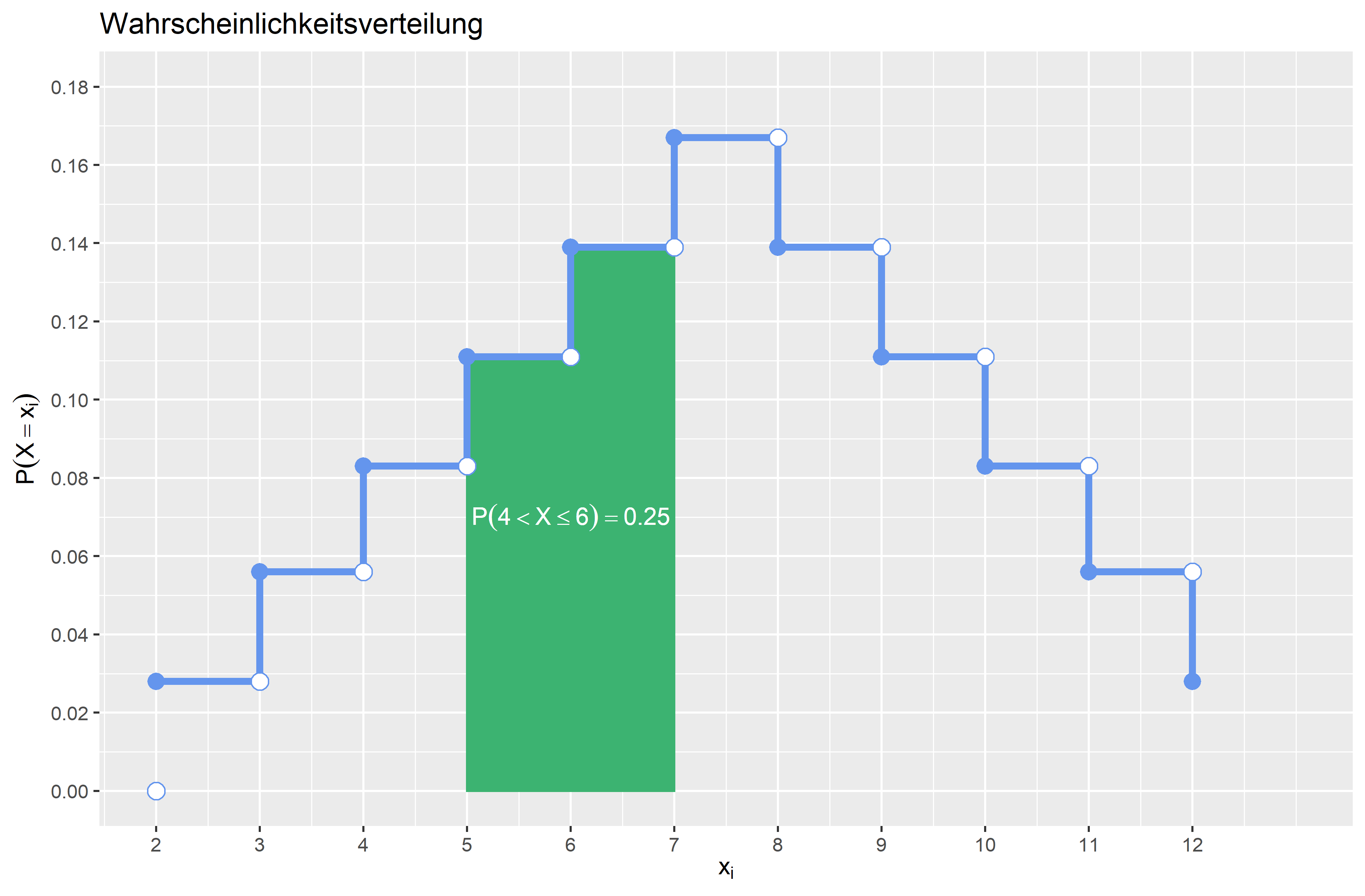
\(P(4 < X \leq 6)\) \(P(4 < X \leq 6) = F(6) - F(4) = \frac{15}{36} - \frac{6}{36} = \frac{9}{36} = 0.25\) Die Wahrscheinlichkeit, dass die Augensumme größer als \(4\) und kleiner gleich \(6\) ist, beträgt \(0.25 (25\%)\).
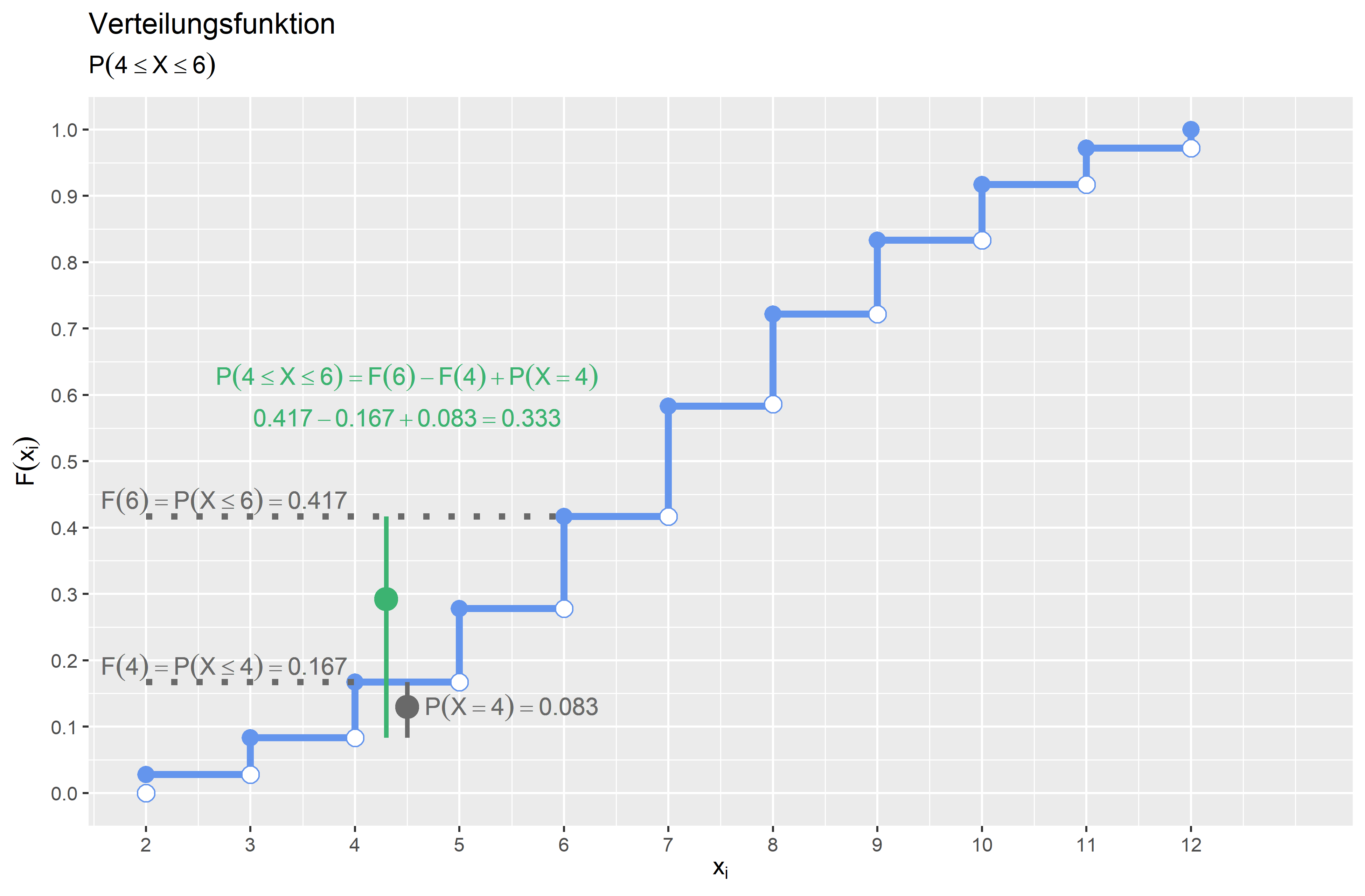
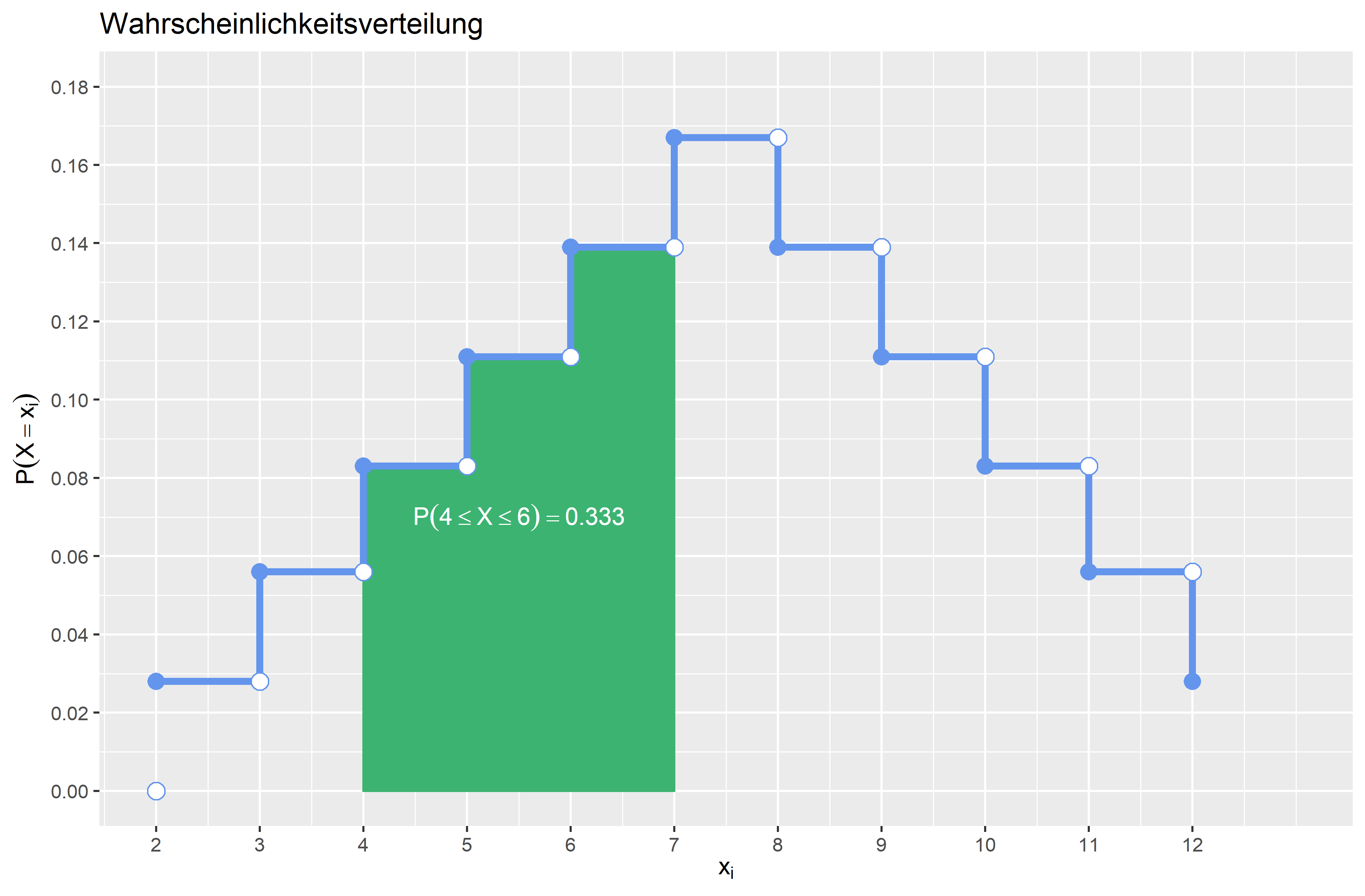
\(P(4 \leq X \leq 6)\) \(P(4 \leq X \leq 6) = F(6) - F(4) + P(X =4) = \frac{15}{36} - \frac{6}{36} + \frac{3}{36} = \frac{12}{36} \approx 0.333\) Die Wahrscheinlichkeit, dass die Augensumme größer gleich \(4\) und kleiner gleich \(6\) ist, beträgt \(0.333 (33.3\%)\).
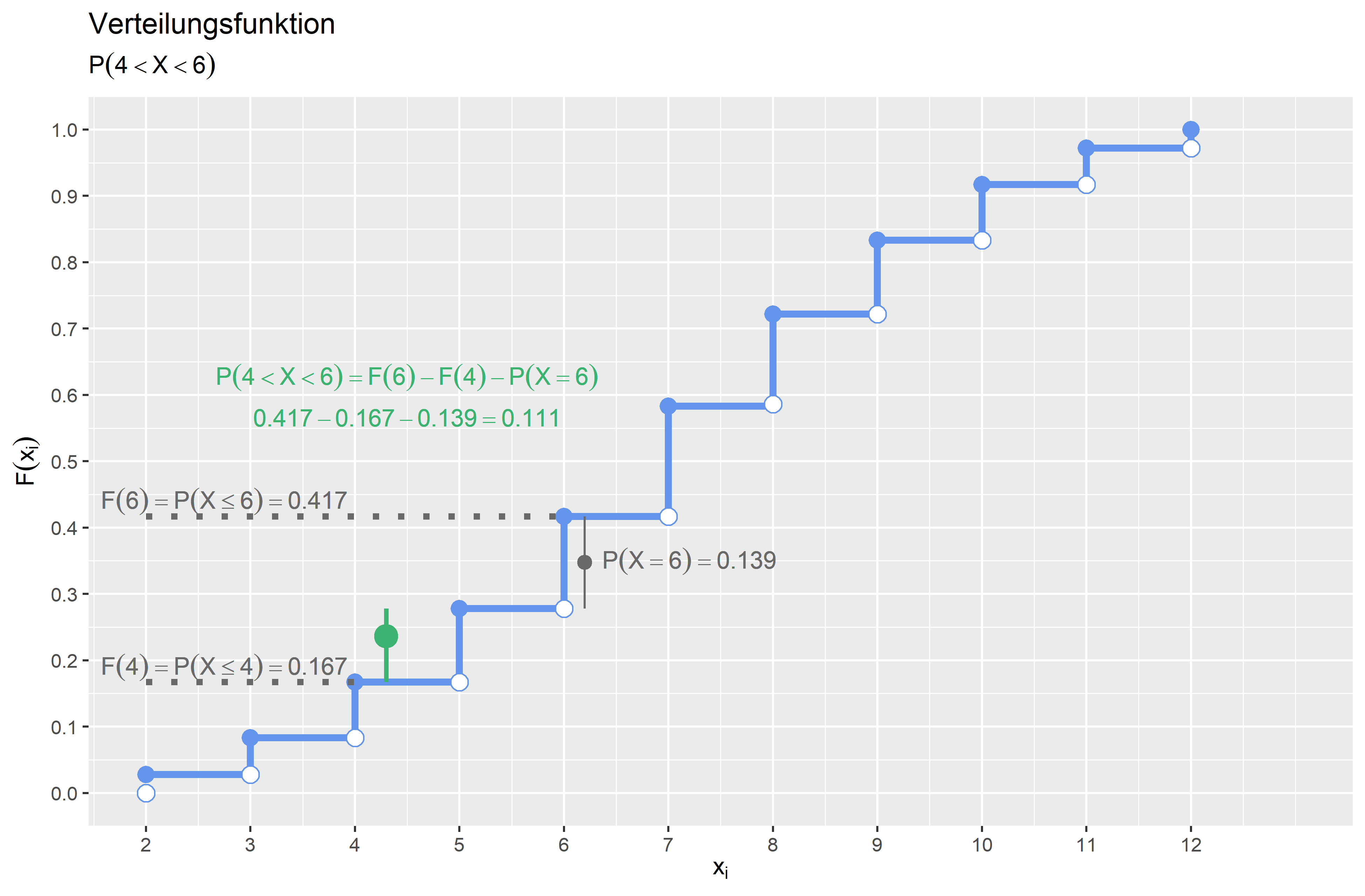
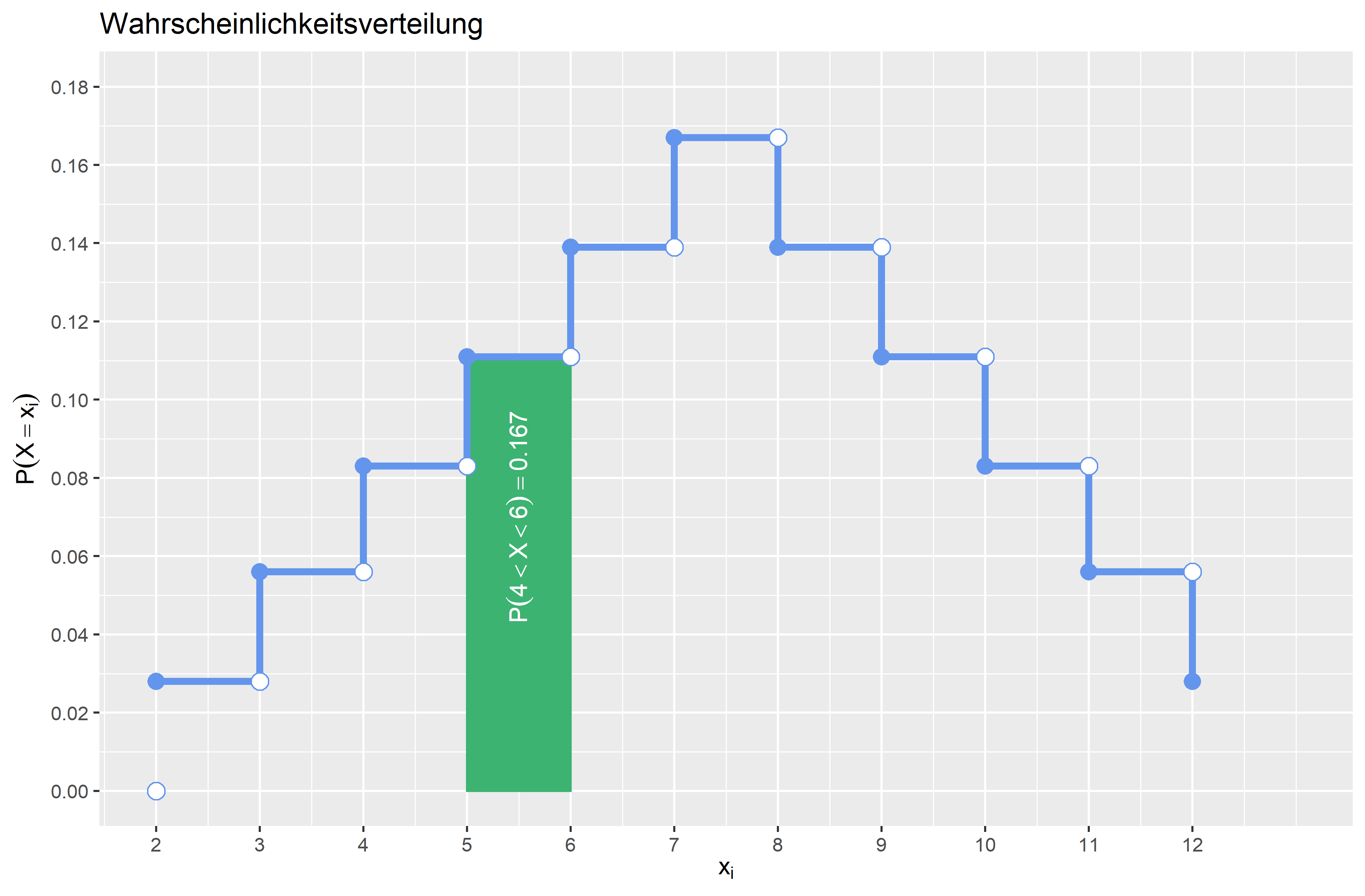
\(P(4 < X <6)\) \(P(4 < X < 6) = F(6)- F(4) -P(X=6) = \frac{15}{36} - \frac{6}{36} - \frac{5}{36} = \frac{4}{36} \approx 0.111\) Die Wahrscheinlichkeit, dass die Augensumme größer als \(4\) und kleiner als \(6\) ist, beträgt \(0.111 (11.1\%)\).
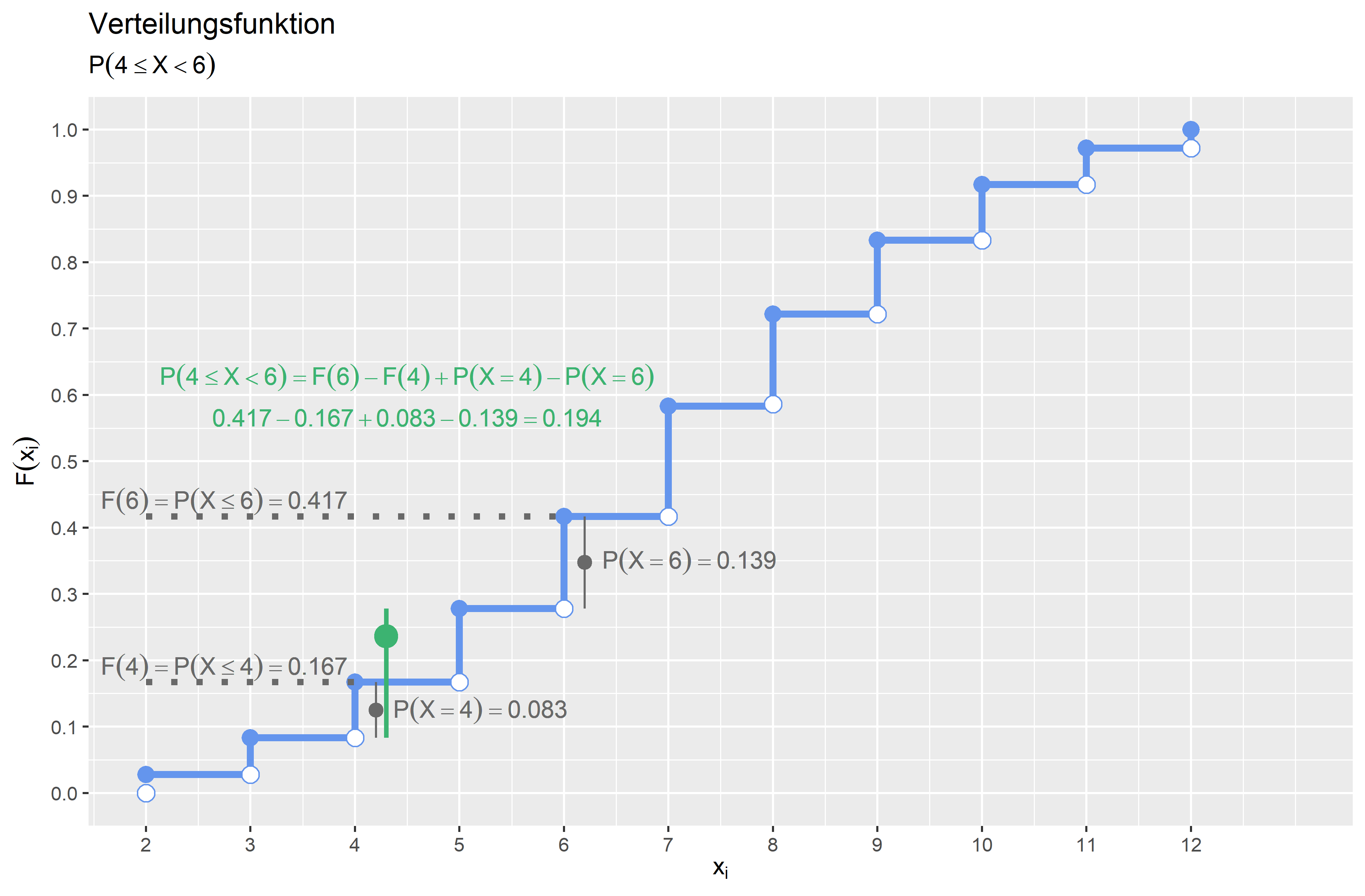
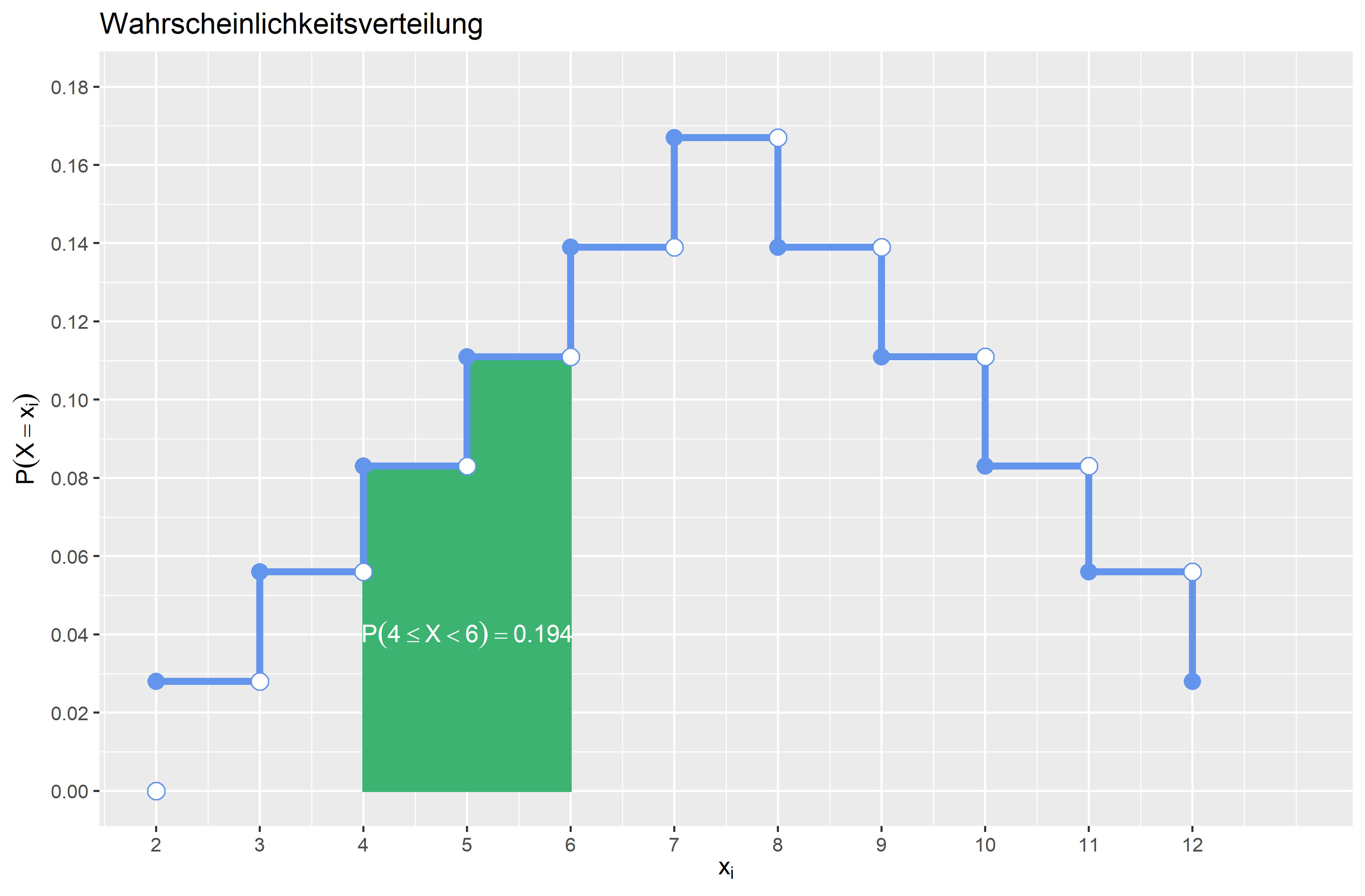
\(P(4 \leq X < 6)\) \(P(4 \leq X < 6) = F(6)-F(4) + P(X=4) - P(X=6) = \frac{15}{36} - \frac{6}{36} + \frac{3}{36} - \frac{5}{36} = \frac{7}{36} \approx 0.194\) Die Wahrscheinlichkeit, dass die Augensumme größer gleich \(4\) und kleiner als \(6\) ist, beträgt \(0.194 (19.4\%)\).
In den Grafiken können Sie zuerst einen Teil der Rechenschritte in der Verteilungsfunktion und Wahrscheinlichkeitsfunktion nachverfolgen.
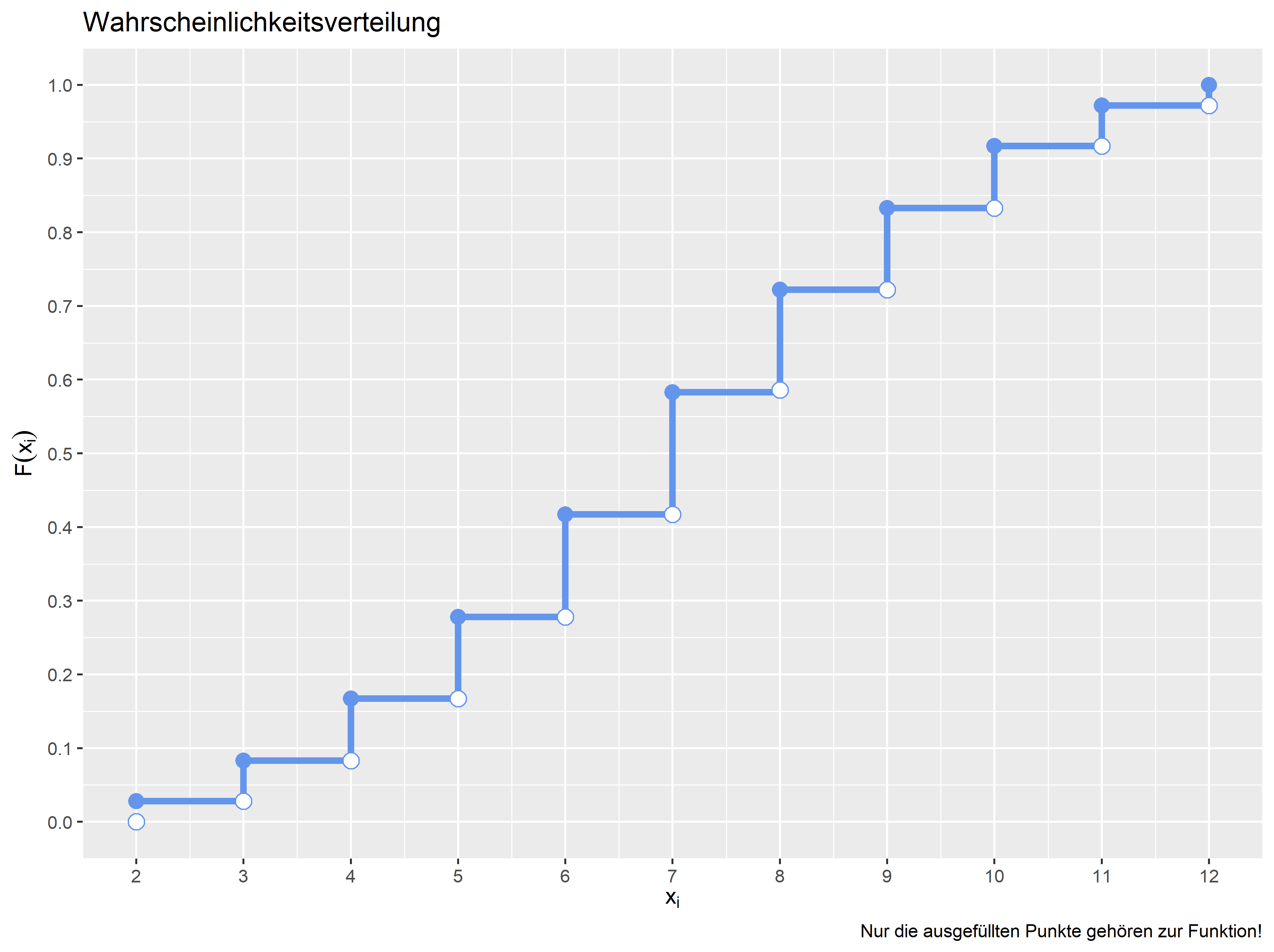
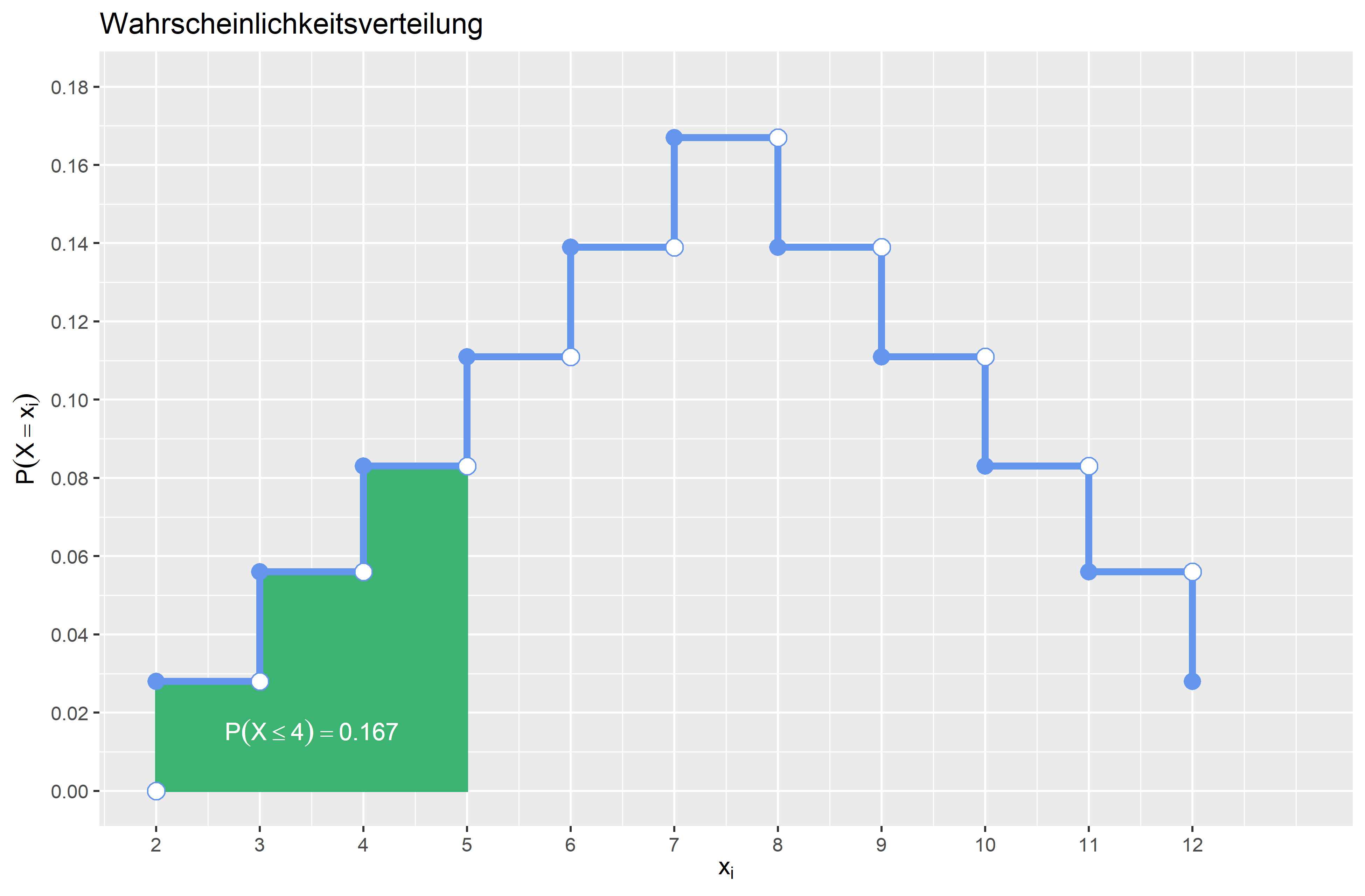
Auf der nächsten Seite berechnen wir nun die Wahrscheinlichkeit für stetige Zufallsvariablen.
Siehe auch: Bortz & Schuster (2010, Kapitel 5.1, 5.2).