Chi-Quadrat-Unabhängigkeitstest
Die Indifferenztabelle ist die Grundlage der Berechnung von \(\chi^2\) (Chi-Quadrat), welches ein Maß zur Bewertung der Unabhängigkeit zwischen zwei Variablen ist. Das untenstehende Rechenbeispiel wird auf der nächsten Seite in einem Lernvideo nochmals erklärt.
Je stärker sich erwartete (Indifferenztabelle) und beobachtete Häufigkeiten (Kontingenztabelle) voneinander unterscheiden, desto stärker ist der Zusammenhang zwischen beiden Variablen.
Die beobachtete Häufigkeit wird hierbei mit \(f_b\) bezeichnet und die erwartete Häufigkeit mit \(f_e\). Vereinfacht ausgedrückt werden die tatsächlich beobachteten absoluten Häufigkeiten ins Verhältnis zu den erwarteten absoluten Häufigkeiten gesetzt.
Hier zum Verständnis die Tabelle mit den erwarteten und beobachteten Häufigkeiten:
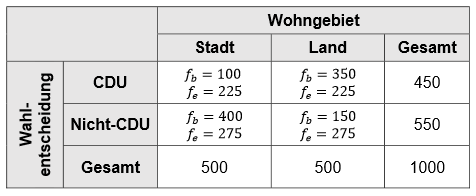
Als Residuum wird dabei die Differenz zwischen \(f_b\) und \(f_e\) bezeichnet, die für jedes Feld berechnet werden muss (\(res=f_b – f_e\)).
Die Formel zur Berechnung von \(\chi^2\) (Chi-Quadrat) lautet daher:
\[\chi^2 = \sum_{i=1}^k \sum_{j=1}^m \frac{(f_{b_{ij}} – f_{e_{ij}})^2}{f_{e_{ij}}}\]
\(i\) ist dabei der Laufindex für die Zeilen und \(j\) der Laufindex für die Spalten.
Im Beispiel ergibt sich daher folgende Rechnung:
\[ \begin{align*} \chi^2 &= \sum_{i=1}^k \sum_{j=1}^m \frac{(f_{b_{ij}} – f_{e_{ij}})^2}{f_{e_{ij}}} \\ &=\frac {(100-225)^2}{225} + \frac{(400-275)^2}{275} + \frac {(350-225)^2}{225} + \frac {(150-275)^2}{275} \\ &\approx 69,44 + 56,82 + 69,44 + 56,82 \\ &\approx 252,53 \end{align*}\]
\(\chi^2\) (Chi-Quadrat) weist einen Wertebereich von \(0\) bis \(+\infty\) (\(\chi^2 \in [0;+\infty]\)) auf. Ein \(\chi^2\) (Chi-Quadrat)-Wert von \(0\) würde bedeuten, dass zwischen den beiden Variablen kein Zusammenhang besteht. Diese Maßzahl ist abhängig von der Fallzahl und der Tabellengröße. Außerdem können \(\chi^2\) (Chi-Quadrat)-Werte unterschiedlicher Tabellengrößen nicht miteinander verglichen werden.
In unserem Beispiel sehen wir, dass der Wert deutlich von \(0\) entfernt ist und somit keine Unabhängigkeit vorliegt. Die drei nachfolgenden Zusammenhangsmaße beruhen auf \(\chi^2\) und werden im weiteren Verlauf vorgestellt:
Phi-Koeffizient (2x2 Kreuztabelle)
Cramers V (jede mögliche Kreuztabelle)
Kontingenzkoeffizient C (jede mögliche Kreuztabelle)