Zentrales Grenzwerttheorem
Wenn man theoretisch unendlich viele Stichproben vom jeweils gleichen Umfang \(n\) aus derselben Population zieht, ergibt sich für die Verteilung der Mittelwerte der Stichproben folgendes Bild.
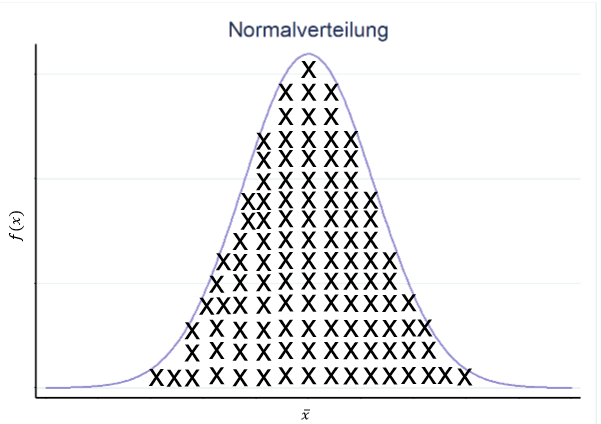
Jedes \(x\) in der Grafik stellt den Mittelwert des Alters (\(\bar{x}_{Alter}\)) einer Stichprobe dar. Auf der \(y\)-Achse ist die Häufigkeit dargestellt, auf der \(x\)-Achse die einzelnen Mittelwerte der Stichproben. Wie angenommen weisen die einzelnen Stichprobenmittelwerte unterschiedliche Werte auf. Allerdings erkennt man ebenso, dass sich die Verteilung dieser Mittelwerte als Normalverteilung darstellt.
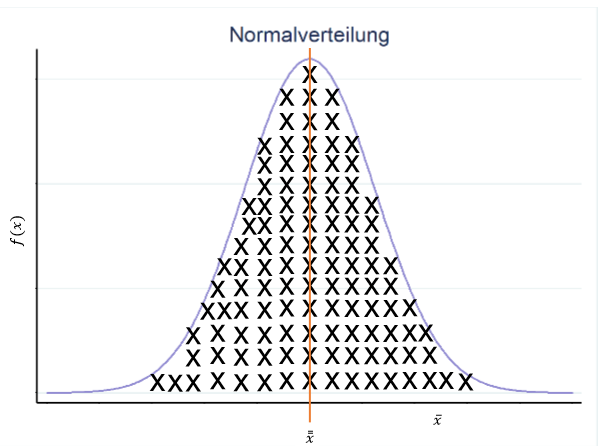
Der berechnete Mittelwerte dieser Stichprobenkennwerteverteilung lautet \(\bar{\bar{x}}\), da er der Mittelwert der Mittelwerte ist. Dieser Mittelwert der Mittelwerte halbiert die Stichprobenkennwerteverteilung und ist am wahrscheinlichsten, da er gleichzeitig den Modus und Median der Verteilung darstellt. Dieser Mittelwert der Mittelwerte (\(\bar{\bar{x}}\)) wird auch Erwartungswert \(E(\bar{x})\) genannt.
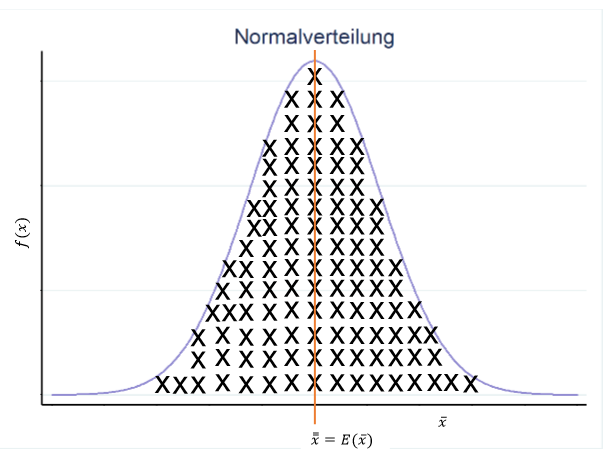
Bei unendlich vielen Stichproben nähert sich dieser Wert dem wahren Wert der Grundgesamtheit \(\mu\) an.
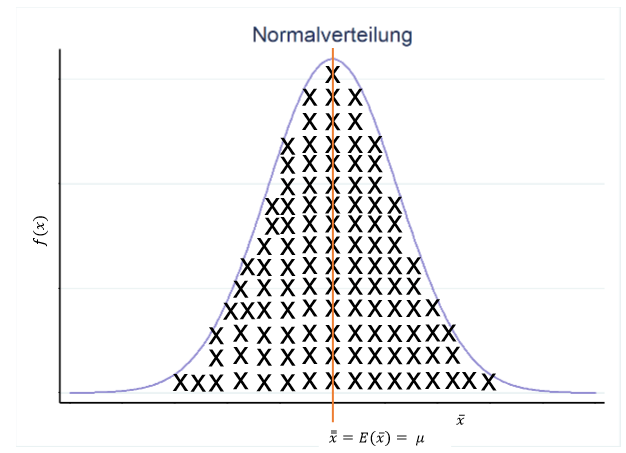
Durch Monte-Carlo-Berechnungen lässt sich beweisen, dass dieser Erwartungswert dem Populationsmittelwert \(\mu\) entspricht. Man spricht daher von einem erwartungstreuen Schätzer. Das was bis hierhin beschrieben wurde, beschreibt das zentrale Grenzwerttheorem. Dieses ist wie folgt definiert: Eine Stichprobenverteilung der Mittelwerte von unendlich vielen Stichproben nähert sich der Normalverteilung asymptotisch an, unabhängig von der Form der zugrundeliegenden Verteilung Daten. Voraussetzung ist, dass die Daten unabhängig und identisch verteilt sind.
Formal ausgedrückt lautet das zentrale Grenzwerttheorem: \(\frac {\bar{x} - \mu}{\frac{s}{\sqrt{n}}} \sim \mathcal{N}(0,1)\)
Aufgrund der zentralen Tendenz werden sich die Mittelwerte um den Populationsmittelwert scharen, erwartungsgemäß gibt es einige Abweichungen. Generell gilt, dass eine größere Stichprobe in aller Regel besser repräsentiert, so dass Mittelwerte sich auf Basis relativ großer Stichproben nah um den Populationsmittelwert scharen. Daher können wir dank des zentralen Grenzwerttheorems Hypothesentests durchführen, auch wenn die Grundgesamtheit nicht normalverteilt ist, sofern die Stichprobe ausreichend groß ist. Mittelwerte auf Basis relativ kleiner Stichproben können stärker um den Populationsmittelwert streuen. Die Berechnung des Stichprobenfehlers der Stichprobenkennwerteverteilung ist ein Maß der Güte der Schätzung. Dieser berechnet die Streuung der Stichprobenkennwerteverteilung. Also im Beispiel, wie sehr die einzelnen Mittelwerte um den Mittelwert der Stichprobenkennwerteverteilung streuen. Dieser Stichprobenfehlers (auch Standardfehler) wird über folgende Formel berechnet:
\(\sigma_{\bar{x}} = \sqrt{ \frac{\sigma^2_{x} } {n} } = \frac{ \sigma_{x}} { \sqrt{n}}\)
Der Standardfehler wird aus der Populationsvarianz des Merkmals \(x\) (\(\sigma^2_{x}\)) durch den Stichprobenumfang \(n\) geteilt. Auch ist es möglich, die Standardabweichung der Population (\(\sigma_{x}\)) durch die Wurzel der Stichprobengröße (\(\sqrt {n}\)) zu teilen und damit den Standardfehler zu berechnen. Der Standardfehler steigt mit steigender Varianz und mit sinkender Stichprobengröße. Daher lohnt es sich, große Stichproben zu ziehen, da der Standardfehler dann sinkt. Die Populationsvarianz ist in der Regel nicht bekannt und wird daher geschätzt. Die Populationsvarianz wird wie folgt geschätzt:
\(\hat{\sigma}^2_{x} = \frac{ \sum\limits_{i=1}^n (x_{i} - \bar{x})^2} {n-1}\)
Der jeweilige Rohwert der Person \(i\) wird zu ihrem Mittelwert (\(\bar{x}_{i}\)) in Betracht gezogen und mit den Werten aller Einheiten summiert. Anschließend wird diese Summe durch die Stichprobengröße minus 1 geteilt. Ein relativ kleiner (großer) Standardfehler bedeutet, dass die Stichprobenmittelwerte alle relativ ähnlich (unähnlich) sind, d.h. grafisch wenig (stark) streuen. Wie anhand der Formel zu erkennen, ist der Standardfehler beeinflusst durch die Varianz des Merkmals in der Population bzw. die Stichprobengröße.