Eta-Quadrat

Mit η2\eta^2 ist ein PRE-Maß und wird angewendet, um den Zusammenhang zweier Merkmale, von denen eine Variable ein metrisches Skalenniveau aufweist und die andere ein nominales Skalenniveau besitzt.

η2\eta^2 beruht auf der Zerlegung der Quadratsummen: Wir können die Gesamt-Quadratsumme in zwei Teile zerlegen. Zum einen wird die Quadratsumme innerhalb der Gruppen (der nominalen oder ordinalen Variable) gebildet. Dies ist die Summe der quadrierten Abweichungen der Werte in den einzelnen Gruppen vom Gruppenmittelwert. Zum anderen kann die Summe der quadrierten Abweichungen der Gruppenmittelwerte vom Gesamtmittelwert gebildetet werden. Dies stellt die Quadratsumme zwischen den Gruppen dar.

Für η2\eta^2 gilt folgendes: η2=QSzwischenQSgesamt=QSzwischenQSzwischen+QSin\eta^2 = \frac {QS_{zwischen}}{QS_{gesamt}}= \frac{QS_{zwischen}}{QS_{zwischen} + QS_{in}}

Gibt es keine Unterschiede zwischen den Gruppen, so erreicht man auch bei Kenntnis der Gruppenzugehörigkeit keine Verbesserung der Vorhersage (QSzwischen=0QS_{zwischen} = 0). Je größer aber die Unterschiede zwischen den Gruppen (QSzwischen>0QS_{zwischen} > 0) relativ zu den Unterschieden innerhalb der Gruppen sind, desto besser wird die Vorhersage.

Für die Interpretation von η2\eta^2 gelten folgende Daumenregeln (Cohen 1998):

  • η2<0.01\eta^2 < 0.01 kein Zusammenhang

  • 0.01≤η2<0.040.01 \leq \eta^2 < 0.04 geringer Zusammenhang

  • 0.04≤η2<0.160.04 \leq \eta^2 < 0.16 mittlerer Zusammenhang und

  • 0.16≤η20.16 \leq \eta^2 starker Zusammenhang

Nehmen wir dazu ein Rechenbeispiel auf: Wir möchten den Zusammenhang zwischen Zufriedenheit mit der Demokratie und dem Geschlecht prüfen. Zu Illustatrionszwecken nehmen wir folgendes Beispiel der Tabelle auf:

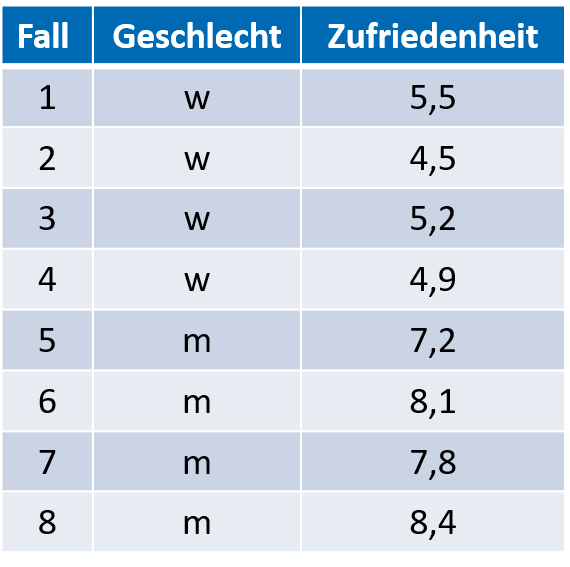
Beispiel Eta
Beispiel Eta

Zur Berechnung von η2\eta^2 gehen wir in vier Schritten vor:

  1. Mittelwerte berechnen

  2. quadrierte Abweichungen innerhalb der Gruppen berechnen und summieren (QSinQS_{in})

  3. quadrierte Abweichungen der Gruppenmittelwerte vom Gesamtmittelwert berechnen und summieren (QSzwischenQS_{zwischen})

  4. η2\eta^2 berechnen

  5. Mittelwerte berechnen

  1. Frauen xˉw=5.5+4.5+5.2+4.94=5.025\bar{x}_w = \frac{5.5 + 4.5 + 5.2 + 4.9}{4} = 5.025
  2. Männer xˉm=7.2+8.1+7.8+8.44=7.875\bar{x}_m = \frac{7.2 + 8.1 + 7.8 + 8.4}{4} = 7.875
  3. gesamt xˉ=5.5+4.5+5.2+4.9+7.2+8.1+7.8+8.48=6.45\bar{x} = \frac{5.5+4.5+5.2+4.9+7.2+8.1+7.8+8.4}{8} = 6.45
  1. quadrierte Abweichungen innerhalb der Gruppen berechnen und summieren (QSinQS_in)
  1. Frauen QSinw=(5.5−5.025)2+(4.5−5.025)2+(5.2−5.025)2+(4.9−5.025)2=0.5475QS_{in_w}= (5.5 - 5.025)^2 + (4.5 - 5.025)^2 + ( 5.2 - 5.025)^2 + (4.9 - 5.025)^2 = 0.5475
  2. Männer QSinm=(7.2−7.875)2+(8.1−7.875)2+(7.8−7.875)2+(8.4−7.875)2=0.7875QS_{in_m} = (7.2 - 7.875)^2 + (8.1-7.875)^2 +(7.8-7.875)^2 + (8.4-7.875)^2 = 0.7875

Summe QSin=QSinw+QSinm=0.5475+0.7875=1.335QS_{in} = QS_{in_w} + QS_{in_m} = 0.5475 + 0.7875 = 1.335

  1. quadrierte Abweichungen der Gruppenmittelwerte vom Gesamtmittelwert berechnen und summieren (QSzwischenQS_{zwischen})
  1. Frauen nw∗(xwˉ−xˉ)2=4∗(5.025−6.45)2=8.1225n_w * (\bar{x_w} - \bar{x})^2= 4 * (5.025-6.45)^2 = 8.1225
  2. Männer nm∗(xmˉ−xˉ)2=4∗(7.875−6.45)2=8.1225n_m * (\bar{x_m} - \bar{x})^2= 4 * (7.875-6.45)^2 = 8.1225

Summe: QSzwischen=8.1225+8.1225=16.245QS_{zwischen} = 8.1225 + 8.1225 = 16.245

  1. η2\eta^2 berechnen η2=QSzwischenQSgesamt=QSzwischenQSzwischen+QSin=16.24516.245+1.335≈0.924\eta^2 = \frac {QS_{zwischen}}{QS_{gesamt}} = \frac {QS_{zwischen}}{QS_{zwischen} + QS_{in}}= \frac{16.245}{16.245 + 1.335} \approx 0.924

Wir haben also ein η2≈0.924\eta^2 \approx 0.924, das auf einen starken Zusammenhang hinweist. Dies liegt u.a. daran, dass wir in den Gruppen kaum Varianz vorliegen haben.