Häufigkeitstabelle
Eine univariate Datenanalyse in tabellarischer Form ergibt eine Häufigkeitstabelle. Diese Häufigkeitstabelle beschreibt, wie sich die Personen auf die Ausprägungen des einen Merkmals verteilen. Nehmen wir das Beispiel der Urliste von der vorherigen Seite wieder auf: Die Variable Augenfarbe (\(X\)) hat die Ausprägungen grün, blau und braun. Dieses Merkmal \(X\) umfasst mehrere Merkmalsausprägungen, in unserem konkreten Fall \(3\) (grün, blau und braun).
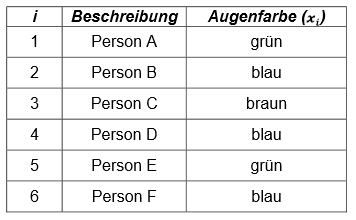
In der Notation werden die Fälle einer Variablen wie folgt zusammengefasst: \(i \in {1, 2, …, n}\). Wobei die Werte des Index \(i\) von \(1\) bis \(n\) (Anzahl Fälle) gehen. Der fünfte Fall (\(i=5\)) ist Person E und diese hat eine grüne Augenfarbe (\(x_{5}=grün\)).
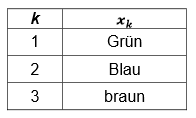
Um die Ausprägungen einer Variable \(X\) zu unterscheiden, wird ein zusätzlicher Laufindex \(k\) verwendet. Jede Variable \(X\) besitzt \(m\) Ausprägungen, somit gilt \(k \in {1, 2, …, n}\).
In unserem Beispiel hat der Laufindex \(k\) den Maximalwert \(3\) (\(m=3\)), da \(3\) verschiedene Ausprägungen vorliegen. Die Ausprägungen einer Variablen werden daher auch mit \(x_k\) angegeben.
In anderen Lehrbüchern wird für die Angabe der Ausprägungen einer Variable der griechische Buchstabe \(\xi\) (xi) oder der Buchstabe \(a\) verwendet. Auch hier gilt, dass beide Angaben einen Laufindex \(k\) besitzen, der die Anzahl der Ausprägungen beinhalten: also \(\xi_k\) oder \(a_k\), wobei \(k\) \(m\) Ausprägungen hat (\(k \in 1, ..., m\)). In unserem Fall liegen wie gesagt \(3\) Ausprägungen vor:
Die Häufigkeit wird mit \(f\) oder \(H\) angegeben. Die absoluten Häufigkeiten geben die Anzahl der Fälle pro Merkmalsausprägung (\(x_k\)) der interessierenden Variablen (\(X\)) wieder. Sie werden daher mit \(f_{x_k}\) oder \(H_{x_k}\) angegeben.
In Lehrbüchern, die für die Ausprägungen \(\xi\) oder \(a\) nutzen, wird die absolute Häufigkeit oft mit folgendem angegeben: \(h_{\xi_k}\) bzw. \(h_{a_k}\).

Die absolute Häufigkeit der Ausprägung grün (\(k=1\)) ist im Beispiel also:
\[f_{x_1} = H_{x_1} = h_{\xi_1} = h_{a_1} = 2\]
Neben den absoluten Häufigkeiten finden sich in Häufigkeitstabellen auch oftmals relative Häufigkeiten wieder. Diese geben uns Information über die Häufigkeit in Bezug zur Gesamtzahl der Fälle. Relative Häufigkeiten werden mit \(h\) bezeichnet. Sie sind der prozentuale Anteil der Ausprägung an allen Fällen und werden wie folgt berechnet: \(h_{x_k} = \frac {H_{x_k}} {n}\), wobei \(n\) die Gesamtzahl der Fälle ist und \(H_{x_k}\) die jeweilige absolute Häufigkeit der Merkmalsausprägung \(k\).
In Lehrbüchern, die \(\xi\) und \(a\) zur Darstellung von Ausprägungen nutzen, werden die relativen Häufigkeiten oft mit \(p_{\xi_k} = \frac{h_{\xi_k}}{n}\) bzw. \(p_{a_k} = \frac{h_{a_k}}{n}\) angegeben

Relative Häufigkeiten sind somit der Anteil der Ausprägung an allen Fällen und somit Prozentwerte: \(33.3\%\) der Befragten eine grüne Augenfarbe (\(h_{x_1} = p_{\xi_1} = p_{a_1} \approx 0.333\)), \(50\%\) der Befragten haben eine blaue Augenfarbe (\(h_{x_2} = p_{\xi_2} = p_{a_2} = 0.5\)) und \(16.7\%\) der Befragten eine braune Augenfarbe (\(h_{x_3} = p_{\xi_3} = p_{a_3} \approx 0.167\)).
Siehe auch: Gehring & Weins (2009, Kapitel 6)