z-Standardisierung
Die z-Transformation wird auch als Standardisierung bezeichnet. Nach der Transformation sind die Werte nicht mehr in den Originalmaßeinheiten gemessen, sondern in Vielfachen der Standardabweichung des Merkmals.
Aus Rohwerten (\(x\)-Werte) kann häufig nur sehr bedingt auf deren relative Position innerhalb einer Verteilung geschlossen werden, das arithmetische Mittel und die Standardabweichung vermitteln zusätzliche Informationen. Werden Rohwerte in z-Werte transformiert, erhält man anhand der Berücksichtigung des arithmetischen Mittels und der Standardabweichung exakte Informationen über die relative Position des jeweiligen Rohwertes. Der Mittelwert von z-transformierten Merkmalen ist immer \(0\) (\(\bar{x}=0\)).
Die z-Transformation wird wie folgt berechnet:
\[z_i = \frac{x_i - \bar{x}}{s}\]
Das Vorzeichen z-transformierter Werte gibt an, ob sich der jeweilige Wert oberhalb (\(+\)) oder unterhalb (\(−\)) des Mittelwertes befindet, der numerische Wert informiert über die Distanz zwischen dem Rohwert und dessen Mittelwert in Standardabweichungseinheiten. Der Mittelwert aller z-Werte ist immer \(0\), Varianz und Standardabweichung sind immer \(1\) (\(\bar{x}=0, s^2=s =1\)).
Ein z-Wert von \(1.5\) bedeutet, dass der entsprechende \(x\)-Wert \(1.5\) Standardabweichungen oberhalb des Mittelwertes liegt. Ein z-Wert von \(−0.5\) dagegen bedeutet, dass der entsprechende \(x\)-Wert \(0.5\) Standardabweichungen unterhalb des Mittelwertes liegt.
Durch die z-Transformation gehen zwar Informationen über die absoluten Abstände zwischen Messwerten verloren, gleichzeitig gewinnt man Informationen über die relativen Abstände zwischen Messwerten. Gleichzeitig lässt sich eine normalverteilte Variable über die z-Transformation in eine Standardnormalverteilung transformieren (\(\bar{x}=0, s^2 =s=1\)).
Im folgenden Lernvideo sehen Sie ein Beispiel der z-Standardisierung. Alternativ finden Sie unterhalb des Lernvideos ein weiteres Textbeispiel.
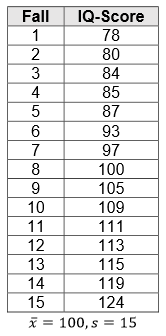
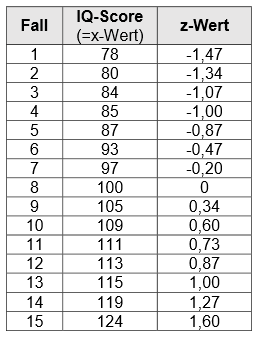
Beispiel: Bei einer Verteilung von IQ-Werten mit \(\bar{x}=100\) und \(s=15\) würde ein Rohwert \(x=130\) einem z-Wert von \(z=+2,00\) entsprechen.
Da der Wert ein positives Vorzeichen aufweist, liegt der Rohwert oberhalb des Mittelwertes. Der Rohwert befindet sich außerdem zwei Standardabweichungen über dem Mittelwert (da 30 Punkte über Mittelwert).