Median
Der Median ist jene Ausprägung/Wert, welcher die Verteilung genau in zwei gleich große Abschnitte teilt. Der Median ist der Wert, der in einer geordneten Liste genau in der Mitte liegt, d.h. dass sich genauso viele Werte oberhalb wie unterhalb des Wertes befinden (jeweils \(50\%\) der Fälle). Folglich setzt der Median eine Ordnung der Werte voraus und damit ein ordinales Skalenniveau. Sowohl bei der Berechnung des Medians als auch beim ordinalen Skalenniveau sind die Werte der Größe nach sortiert.
Je nachdem, ob man eine ungerade Anzahl an Fällen (\(n\)) oder gerade Anzahl an Fällen hat, wird der Median unterschiedlich berechnet. Das Zeichen für den Median ist: \(\tilde{x}: Median\)
Formel bei ungeradem \(n\): \(\tilde{x}= x_{\frac {n+1}{2}}\)
Formel bei geradem \(n\): \(\tilde{x} =\frac{1}{2} \ast (x_{\frac{n}{2}} + x_{\frac{n}{2}+1})\)
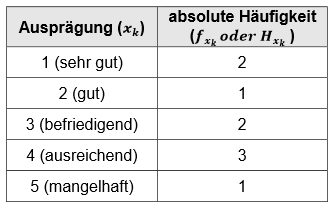
Dazu zwei Rechenbeispiele: Wir betrachten die Schulnoten von \(10\) Personen (\(n=10\)). Wir haben also ein gerades n und wenden die zweite Formel an:

Wir können den Median daher wie folgt berechnen:
\[\tilde{x} =\frac{1}{2} \ast (x_{\frac{n}{2}} + x_{\frac{n}{2}+1})=\frac{1}{2} \ast (x_{\frac{10}{2}} + x_{\frac{10}{2}+1})=\frac{1}{2} \ast (x_5 + x_6)\]
Der Median liegt somit zwischen den Werten an der an der 5. (\(x_5\)) und 6. Stelle (\(x_6\)). Es ist sozusagen der „fünfeinhalbste Wert“. Dazu müssen wir die Werte in eine geordnete Reihe der Fälle bringen:
\[1, 1, 2, 3, 3, 4, 4, 4, 5, 5 = x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9, x_10\]
An der 5. bzw. 6. Stelle dieser geordneten Reihe der Fälle finden wir:
\(x_5 =3\) und \(x_6=4\)
Dies setzt man nun in die Formel von oben ein:
\[\tilde{x}=\frac{1}{2} \ast (x_5 + x_6) = \frac{1}{2} \ast (3+4) = 3.5\]
Daher beträgt der Median der Schulnoten in diesem Beispiel den Wert 3,5 (\(\tilde{x}=3.5\)). Das heißt \(50\%\) der befragten Personen haben eine bessere (kleinere) Note und \(50\%\) haben eine schlechtere (höhere) Note.
Wenn wir die Schulnoten von nur \(9\) Personen (\(n=9\)) betrachten, wenden wir die erste Formel für ein ungerades \(n\) an:
\[\tilde{x} =\frac{1}{2} \ast (x_{\frac{n}{2}} + x_{\frac{n}{2}+1}) = x_{\frac{9+1}{2}}=x_{\frac{10}{2}} = x_{5}\]
Hier ist der Median an der Stelle 5 (\(x_5\)). Dazu müssen wir die Werte wieder in eine geordnete Reihe der Fälle bringen:
\[1, 1, 2, 3, 3, 4, 4, 4, 5 =x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9\]
An der 5. Stelle dieser geordneten Reihe finden wir:
\[x_5 =3\]
Der Median dieser Verteilung liegt als beim Wert 3 (\(\tilde{x}=3\)). \(50\%\) der befragten Personen haben eine bessere (kleinere oder gleichgroße) Note und \(50\%\) haben eine schlechtere (höhere) Note.
Siehe auch: Gehring & Weins (2009, Kapitel 6.1).