Kumulierte Häufigkeiten
Wie im Kapitel Grundbegriffe dargestellt, stellen Häufigkeitstabellen die Darstellung der absoluten und relativen Häufigkeiten der Merkmalsausprägung einer Variablen dar. Neben den absoluten und relativen Häufigkeiten, werden oftmals auch kumulierte relative Häufigkeiten zusätzlich angegeben. Für kumulierte relative Häufigkeiten muss eine Rangordnung zwischen den Ausprägungen vorhanden sein, also mindestens ein ordinales Skalenniveau vorliegen.
Nehmen wir ein Beispiel, bei dem wir von \(100\) Befragten die Anzahl abgefragt haben, in wie viele Länder der Welt sie bereits gereist sind.
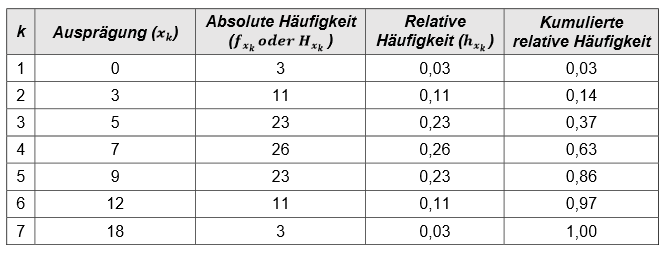
Kumulierte relative Häufigkeiten summieren die jeweiligen relativen Häufigkeiten bis zur jeweiligen Ausprägung auf (\(\sum_{k=1}^m h_{x_k} = \sum_{k=1}^m p_{\xi_k}= \sum_{k=1}^m p_{a_k}\)). Sie geben also an, wie häufig eine bestimmte Ausprägung und alle niedrigeren Ausprägung eines Merkmals beobachtet wurden. Kumulierte relative Häufigkeiten werden auch als Prozentränge bezeichnet. Mithilfe der Ausgabe von kumulierten relativen Häufigkeiten können die Quartile aus der Tabelle abgelesen werden.
Die Quartile können nun anhand der kumulierten relativen Häufigkeiten einfach abgelesen werden: Die Quartile befinden sich an den Werten, an denen der jeweilige Grenzwert des Quartils erreicht oder überschritten wird (\(0.25\) für das untere Quartil, \(0.5\) für den Median bzw. das mittlere Quartil, und \(0.75\) für das obere Quartil).
Für unser Beispiel heißt dies also folgendes:
\[\tilde{x}_{0.25}=x_3=5\]
\[\tilde{x}_{0.5}=\tilde{x}=x_4=7\]
\[\tilde{x}_{0.75}=x_5=9\]
\(25\%\) der Befragten haben maximal fünf Länder bereist, \(50\%\) haben maximal sieben Länder bereist und \(75\%\) haben maximal neun Länder bereist.