Varianz
Die Varianz ist eine Kennzahl, welche die Streuung der Variable ausdrückt und alle Werte berücksichtigt. Sie wird berechnet, indem man den Durchschnitt der quadrierten Abweichung vom arithmetischen Mittel berechnet. Die Varianz beschreibt also den durchschnittlichen quadrierten Abstand zum Mittelwert.
Die Formel zur Anwendung auf eine Vollerhebung ist folgende:
\[\sigma^2=\frac{1}{n} \ast \sum_{i=1}^n(x_i - \bar{x})^2 = \frac{\sum_{i=1}^n(x_i - \bar{x})^2}{n}\]
Wenn nur eine Stichprobe erhoben wird, muss die Formel um \(\frac{1}{n-1}\) korrigiert werden:
\[s^2=\frac{1}{n-1} \ast \sum_{i=1}^n(x_i - \bar{x})^2 = \frac{\sum_{i=1}^n(x_i - \bar{x})^2}{n-1}\]
Im untenstehenden Beispiel berechnen wir die Varianz am Beispiel der Formel für Stichproben. Wir haben von \(10\) Mitarbeitenden das Einkommen abgefragt.
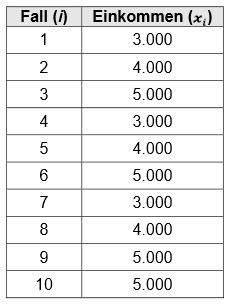
Zuerst müssen wir den Mittelwert berechnen und dann jeweils die Distanz zum Mittelwert für jeden einzelnen Wert.
Der Mittelwert lag im vorliegenden Fall bei \(\bar{x}=4100\).
Nun berechnen wir für jeden Fall die Differenz zum Mittelwert.
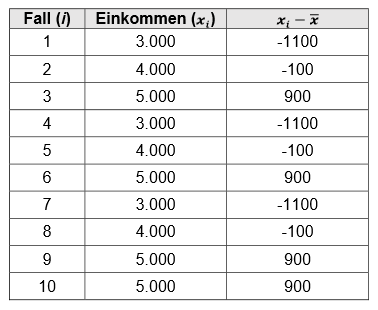
Diese Differenz setzen wir nun jeweils in die Formel der Varianz ein:
\[\begin{align}s^2&=\frac{1}{10-1} \ast \sum_{i=1}^10(x_i - \bar{x})^2 \\ &=\frac{1}{9} \ast ((-1100)^2 + (-100)^2 + 900^2 + (-1100)^2 + (100)^2 + 900^2 + (-1000)^2+ (-100)^2 + 900^2 + 900^2) \\ &= \frac{1}{9} \ast 6900000 \approx 766666.67 \\ \end{align}\]
Die durchschnittliche quadrierte Abweichung beträgt in unserem Beispiel \(766666.67\) (\(s^2=766666.67\)).
Durch das Quadrieren ist die ursprüngliche Maßeinheit (hier Euro) verloren gegangen, so dass die Zahl nicht leicht zu interpretieren ist (vgl. Gehring & Weins, 2009, p. 136). Für weitere statistische Verfahren hat die Berechnung der Varianz große Bedeutung (Bortz & Schuster, 2010, p. 31). Dennoch gilt als Faustregel: Je höher die Varianz, desto weiter liegen die Messwerte voneinander entfernt. Eine Varianz von \(0\) würde bedeuten, dass jeder Messwert gleich dem Mittelwert ist und kein abweichender Messwert vorliegt. Das heißt für alle \(x_i\) mit \(i \in {1, 2, …, n}\) gilt \(x_i=\bar{x}\).
In der Praxis verwendet man vor allem die Wurzel aus der Varianz, die sogenannte Standardabweichung.
Siehe auch: Gehring & Weins (2009, Kapitel 6.2.4)