Perzentile
Perzentile teilen die Ausprägungen der Variablen in gleich große Gruppen, sodass sich in jeder Gruppe der gleiche Prozentsatz an Werten befindet. Häufig genutzt werden die Quartile (= Viertel, jeweils \(25\%\)). Bei Dezilen handelt es sich hingegen um Gruppen von jeweils \(10\%\) der Werte.
Quartile teilen die Verteilung in vier gleich große Viertel: \(25\%\) der Werte sind kleiner oder gleich groß mit dem 1. Quartil oder unterem Quartil (\(\tilde{x}_{0.25}\)), \(50\%\) sind kleiner oder gleich groß wie das 2. Quartil oder mittlere Quartil, das daher gleichzusetzen ist mit dem Median (\(\tilde{x}_{0.5}=\tilde{x}\)) und 75 % sind kleiner oder gleich groß mit dem 3. Quartil oder obere Quartil (\(\tilde{x}_{0.75}\)).
Quartile werden erst ab einer Stichprobengröße von zumindest \(20\) (\(n=20\)) eingesetzt. Die grundsätzliche Berechnung von Perzentilen ist wie folgt:
Wenn \(n*p\) ganzzahlig:
\[\tilde{x}_p = \frac{1}{2} (x_{n*p} + x_{n*p+1})\]
Wenn \(n*p\) nicht ganzzahlig:
\[\tilde{x}_p=x_{\lceil n*p \rceil}\]
Für die Quartile, als gängigste Form der Perzentile, ergeben sich folgende Formeln:
Wenn \(n*0.75\) ganzzahlig:
\[\tilde{x}_{0.75} = \frac{1}{2} (x_{n*0.75} + x_{n*0.75+1}))\]
Wenn \(n*0.75\) nicht ganzzahlig:
\[\tilde{x}_{0.75}=x_{\lceil n*0.75 \rceil}⌉\]
Wenn \(n*0.25\) ganzzahlig:
\[\tilde{x}_{0.75}=x_{\lceil n*0.75 \rceil}\]
Wenn \(n*0.25\) nicht ganzzahlig:
\[\tilde{x}_{0.25}=x_{\lceil n*0.25 \rceil}⌉\]
Das mittlere Quartil ist gleich dem Median:
\[\tilde{x}_{0.5}=\tilde{x}\]
Dies berechnen wir kurz an einem Beispiel: Wir haben \(20\) Studierende (\(n=20\)) befragt nach der Anzahl der politikwissenschaftlichen Bücher, die sie jeweils besitzen.
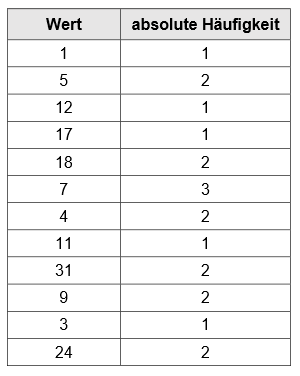
Für die Berechnung eines Perzentils, bzw. im genaueren Fall eines Quartils, müssen die Daten immer in eine geordnete Reihe gesetzt werden:
\[1,3,4,4,5,5,7,7,7,9,9,11,12,17,18,18,24,24,31,31\]
\[x_1, x_2, x_3, x_.4, x_5, x_6, x_7, x_8, x_9, x_{10}, x_{11}, x_{12}, x_{13}, x_{14}, x_{15}, x_{16}, x_{17}, x_{18}, x_{19}, x_{20}\]
Um nun zu wissen, welche Formel wir für die Quartile berechnen müssen, müssen wir zuerst \(n∗p\) berechnen.
\[0.25*20=5\]
\[0.5*20=10\]
\[0.75*20=15\]
Wir erhalten in allen Fällen ganzzahlige Ergebnisse, daher werden die Quartile wie folgt berechnet:
\[\tilde{x}_{0.75} = \frac{1}{2} (x_{n*0.75} + x_{n*0.75+1})\]
\[\tilde{x}_{0.25} = \frac{1}{2} (x_{n*0.25} + x_{n*0.25+1})\]
Für das dritte Quartil (\(75\%\)) ergibt sich daher:
\[\tilde{x}_{0.75} = \frac{1}{2} (x_{n*0.75} + x_{n*0.75+1})=\frac{1}{2} \ast (x_{15} + x_{16})\]
An der 15. bzw. 16. Stellen der geordneten Datenreihe ist: \(x_{15}=18\) und \(x_{16}=18\)
\[\tilde{x}_{0.75} = \frac{1}{2} \ast (x_{15} + x_{16})=\frac{1}{2} \ast (18+18)=18\]
Das obere Quartil hat daher den Wert \(18\) (\(\tilde{x}_{0.75}=18\)).
Für das untere Quartil ergibt sich ebenso:
\[\tilde{x}_{0.25} = \frac{1}{2} (x_{20*0.25} + x_{20*0.25+1})=\frac{1}{2} \ast (x_5 + x_6)\]
An der 5. bzw. 6. Stellen der geordneten Datenreihe ist: \(x_5=5\) und \(x_6=5\)
\[\tilde{x}_{0.25} =\frac{1}{2} \ast (x_5 + x_6)= \frac {1}{2} \ast (5+5) =5\]
Der Wert des unteren Quartils ist daher \(5\) (\(\tilde{x}_{0.25}=5\)).
\(25\%\) der Werte des Merkmals Anzahl politikwissenschaftlicher Bücher sind kleiner/gleich \(5\) und \(75\%\) der Werte des Merkmals sind kleiner/gleich \(18\).
Bei ungeradem Wert von \(n*p\) wird - entsprechend der Formel - der Wert aufgerundet.
Wenn wir nur \(18\) Beobachtungen hätten, wäre \(n*p=18*0.75=13.5\) bzw. \(18*0.25=4.5\).
Das obere Quartil wäre daher \(\tilde{x}_{0.75} = x_{\lceil 13.5 \rceil} =x_{14}\) bzw. das untere Quartil wäre \(\tilde{x}_{0.25}=x_{\lceil 4.5 \rceil}=x_5\).
Siehe auch: Gehring & Weins (2009, pp. 132–135).