Boxplots
Die Darstellung eines Boxplots ist in diesem Lernvideo erklärt. Alternativ können Sie weiter runterscrollen und die Textbeschreibung lesen.
Der Boxplot, auch Box-Whisker-Plot, ist eine kompakte deskriptive Darstellung verschiedener univariater Kennwerte eines Merkmals. Die Fünf-Punkte-Zusammenfassung einer Verteilung inkludiert das Minimum, das 1. Quartil, den Median, das 3. Quartil sowie das Maximum. Boxplots weisen damit eine extrem hohe Informationsdichte auf. Durch diese konzentrierten Informationen erlauben sie eine sehr schnelle Abschätzung der Streuung.
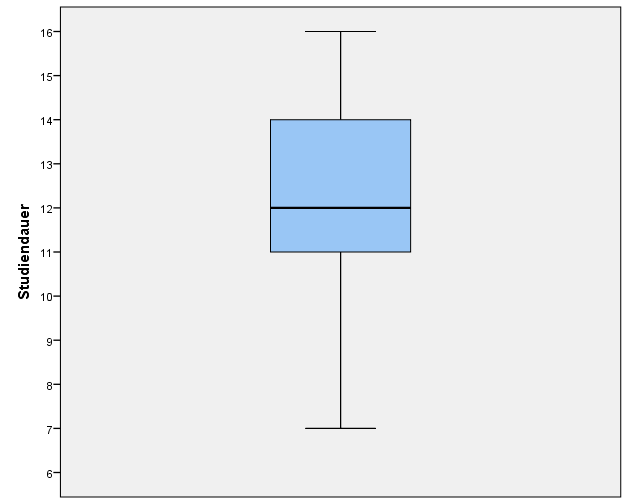
Das Beispiel unten beschreibt beispielhaft die durchschnittliche Semesterzahl eines beliebigen Studiengangs. Grafisch wird diese Beschreibung durch Boxplots visualisiert. Die untere Grenze der Box ist das 1. Quartil (\(11 Semester\)), die obere Grenze der Box ist das 3. Quartil (\(14 Semester\)). Die Länge der Box entspricht dem Interquartilsabstand (\(14 – 11 = 3 Semester\)).
Innerhalb der Box ist der Median (\(12\) Semester) durch eine Linie gekennzeichnet. An der Box erkennt man deutlich, dass die Studiendauer linkssteil verteilt ist. Der Abstand zwischen Median und 3. Quartil ist größer als der Abstand zwischen Median und 1. Quartil.
Die Box wird durch zwei Whisker nach oben und unten verlängert. Diese Begrenzungen entsprechen dem Minimum und Maximum der Verteilung, sofern wie im Beispiel keine Ausreißer existieren. Die Spannweite ist also ebenfalls im Boxplot dargestellt.
Ausreißer sind Messwerte, die weiter als den \(1.5\)-fachen Interquartilsabstand von der Box entfernt sind – sie werden einzeln dargestellt. Sind Ausreißer vorhanden, dann ist der Whisker an der Stelle des kleinsten bzw. größten Messwertes, der kein Ausreißer ist.