arithm. Mittelwert
Der Mittelwert, auch arithmetisches Mittel, gibt den durchschnittlichen Wert einer/s Variable/Merkmals an. Dazu müssen die Abstände zwischen den Werte interpretierbar sein, also muss mindestens Intervallskalenniveau vorliegen.
Der Mittelwert wird berechnet aus der Summe aller Werte, die durch die Anzahl der Werte (n) geteilt wird.
\[\bar{x}=\frac{1}{n} \ast \sum_{i=1}^n x_i = \frac{\sum_{i=1}^n x_i}{n}\]
Werte, die weit von den restlichen Werten abweichen, verzerren dieses Maß der zentralen Tendenz. Der Mittelwert ist daher anfällig für Ausreißer und nicht gut geeignet, um schiefe Verteilungen (mit Extremwerten) zu beschreiben.
Dazu kurz ein Rechenbeispiel: Nehmen wir eine Verteilung von \(10\) Personen für das Einkommen an:
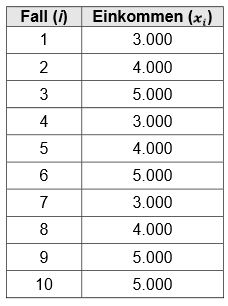
Der Mittelwert berechnet sich wie folgt:
\[\bar{x}=\frac{1}{n} \ast \sum_{i=1}^n x_i = \frac{\sum_{i=1}^n x_i}{n}\]
\[=\frac{1}{10} \ast (3000+4000+5000+3000+4000+5000+3000+4000+5000+5000)=4100\]
Wenn wir nun dieser Verteilung einen Ausreißer hinzufügen ergibt sich folgendes Bild:
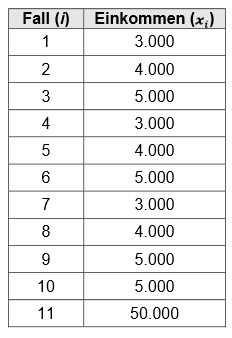
\[\bar{x}=\frac{1}{n} \ast \sum_{i=1}^n x_i =\frac{1}{11} \ast (x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7 + x_8 + x_9 + x_{10} + x_{11})\]
\[=\frac{1}{11} \ast (3000+4000+5000+3000+4000+5000+3000+4000+5000+5000+50000) \approx 8273\]
Ein einziger Fall erhöht somit das arithmetische Mittel um ca. \(4173\).
Zur Beschreibung von Verteilungen mit Extremwerten ist daher der Median besser geeignet.
Siehe auch: Gehring & Weins (2009, Kapitel 6.1)